题目内容
（2013•南京）如图，在四边形ABCD中，AB=BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N．（1）求证：∠ADB=∠CDB；
（2）若∠ADC=90°，求证：四边形MPND是正方形．
分析：（1）根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD，由全等三角形的性质即可得到：∠ADB=∠CDB；
（2）若∠ADC=90°，由（1）中的条件可得四边形MPND是矩形，再根据两边相等的四边形是正方形即可证明四边形MPND是正方形．
（2）若∠ADC=90°，由（1）中的条件可得四边形MPND是矩形，再根据两边相等的四边形是正方形即可证明四边形MPND是正方形．
解答：证明：（1）∵对角线BD平分∠ABC，
∴∠ABD=∠CBD，
在△ABD和△CBD中，
，
∴△ABD≌△CBD，
∴∠ADB=∠CDB；
（2）∵PM⊥AD，PN⊥CD，∠ADB=∠CDB，
∴∠PMD=∠PND=90°，PM=PN，
∵∠ADC=90°，
∴四边形MPND是矩形，
∵PM=PN，
∴四边形MPND是正方形．
∴∠ABD=∠CBD，
在△ABD和△CBD中，
|
∴△ABD≌△CBD，
∴∠ADB=∠CDB；
（2）∵PM⊥AD，PN⊥CD，∠ADB=∠CDB，
∴∠PMD=∠PND=90°，PM=PN，
∵∠ADC=90°，
∴四边形MPND是矩形，
∵PM=PN，
∴四边形MPND是正方形．
点评：本题考查了全等三角形的判定和性质、角平分线的性质、矩形的判定和性质以及正方形的判定，解题的关键是熟记各种几何图形的性质和判定．
练习册系列答案
阅读快车系列答案
相关题目
（2013•南京）如图，⊙O1，⊙O2的圆心在直线l上，⊙O1的半径为2cm，⊙O2的半径为3cm．O1O2=8cm，⊙O1以1cm/s的速度沿直线l向右运动，7s后停止运动．在此过程中，⊙O1和⊙O2没有出现的位置关系是（ ）
（2013•南京）如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°＜α＜90°），若∠1=110°，则∠α=
（2013•南京）如图，在梯形ABCD中，AD∥BC，AB=DC，AC与BD相交于P．已知A（2，3），B（1，1），D（4，3），则点P的坐标为（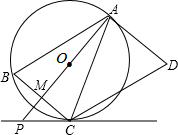
（2013•南京）如图，AD是⊙O的切线，切点为A，AB是⊙O的弦．过点B作BC∥AD，交⊙O于点C，连接AC，过点C作CD∥AB，交AD于点D．连接AO并延长交BC于点M，交过点C的直线于点P，且∠BCP=∠ACD．