题目内容
 (2013•南京)如图,在梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于P.已知A(2,3),B(1,1),D(4,3),则点P的坐标为(
(2013•南京)如图,在梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于P.已知A(2,3),B(1,1),D(4,3),则点P的坐标为(3
3
,| 7 |
| 3 |
| 7 |
| 3 |
分析:过A作AM⊥x轴与M,交BC于N,过P作PE⊥x轴与E,交BC于F,根据点的坐标求出各个线段的长,根据△APD∽△CPB和△CPF∽△CAN得出比例式,即可求出答案.
解答: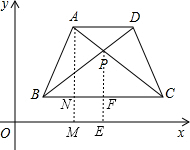
解:过A作AM⊥x轴与M,交BC于N,过P作PE⊥x轴与E,交BC于F,
∵AD∥BC,A(2,3),B(1,1),D(4,3),
∴AD∥BC∥x轴,AM=3,MN=EF=1,AN=3-1=2,AD=4-2=2,BN=2-1=1,
∴C的坐标是(5,1),BC=5-1=4,CN=4-1=3,
∵AD∥BC,
∴△APD∽△CPB,
∴
=
=
=
,
∴
=
∵AM⊥x轴,PE⊥x轴,
∴AM∥PE,
∴△CPF∽△CAN,
∴
=
=
=
,
∵AN=2,CN=3,
∴PF=
,PE=
+1=
,CF=2,BF=2,
∴P的坐标是(3,
),
故答案为:3,
.

解:过A作AM⊥x轴与M,交BC于N,过P作PE⊥x轴与E,交BC于F,
∵AD∥BC,A(2,3),B(1,1),D(4,3),
∴AD∥BC∥x轴,AM=3,MN=EF=1,AN=3-1=2,AD=4-2=2,BN=2-1=1,
∴C的坐标是(5,1),BC=5-1=4,CN=4-1=3,
∵AD∥BC,
∴△APD∽△CPB,
∴
| AD |
| BC |
| AP |
| PC |
| 2 |
| 4 |
| 1 |
| 2 |
∴
| CP |
| AC |
| 2 |
| 3 |
∵AM⊥x轴,PE⊥x轴,
∴AM∥PE,
∴△CPF∽△CAN,
∴
| PF |
| AN |
| CF |
| CN |
| CP |
| CA |
| 2 |
| 3 |
∵AN=2,CN=3,
∴PF=
| 4 |
| 3 |
| 4 |
| 3 |
| 7 |
| 3 |
∴P的坐标是(3,
| 7 |
| 3 |
故答案为:3,
| 7 |
| 3 |
点评:本题考查了坐标与图形性质,梯形的性质,相似三角形的性质和判定的应用,主要是考查学生综合运用知识进行计算的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
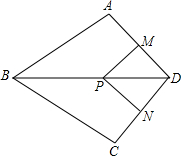 (2013•南京)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(2013•南京)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.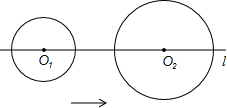 (2013•南京)如图,⊙O1,⊙O2的圆心在直线l上,⊙O1的半径为2cm,⊙O2的半径为3cm.O1O2=8cm,⊙O1以1cm/s的速度沿直线l向右运动,7s后停止运动.在此过程中,⊙O1和⊙O2没有出现的位置关系是( )
(2013•南京)如图,⊙O1,⊙O2的圆心在直线l上,⊙O1的半径为2cm,⊙O2的半径为3cm.O1O2=8cm,⊙O1以1cm/s的速度沿直线l向右运动,7s后停止运动.在此过程中,⊙O1和⊙O2没有出现的位置关系是( ) (2013•南京)如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=
(2013•南京)如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=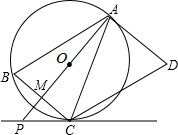 (2013•南京)如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.
(2013•南京)如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.