题目内容
 (2013•南京)如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.
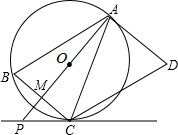
(2013•南京)如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若AB=9,BC=6.求PC的长.
分析:(1)过C点作直径CE,连接EB,由CE为直径得∠E+∠BCE=90°,由AB∥DC得∠ACD=∠BAC,而∠BAC=∠E,∠BCP=∠ACD,所以∠E=∠BCP,于是∠BCP+∠BCE=90°,然后根据切线的判断得到结论;
(2)根据切线的性质得到OA⊥AD,而BC∥AD,则AM⊥BC,根据垂径定理有BM=CM=
BC=3,根据等腰三角形性质有AC=AB=9,在Rt△AMC中根据勾股定理计算出AM=6
;
设⊙O的半径为r,则OC=r,OM=AM-r=6
-r,在Rt△OCM中,根据勾股定理计算出r=
,则CE=2r=
,OM=6
-
=
,利用中位线性质得BE=2OM=
,然后判断Rt△PCM∽Rt△CEB,根据相似比可计算出PC.
(2)根据切线的性质得到OA⊥AD,而BC∥AD,则AM⊥BC,根据垂径定理有BM=CM=
| 1 |
| 2 |
| 2 |
设⊙O的半径为r,则OC=r,OM=AM-r=6
| 2 |
27
| ||
| 8 |
27
| ||
| 4 |
| 2 |
27
| ||
| 8 |
21
| ||
| 8 |
21
| ||
| 4 |
解答: 解:(1)PC与圆O相切,理由为:
解:(1)PC与圆O相切,理由为:
过C点作直径CE,连接EB,如图,
∵CE为直径,
∴∠EBC=90°,即∠E+∠BCE=90°,
∵AB∥DC,
∴∠ACD=∠BAC,
∵∠BAC=∠E,∠BCP=∠ACD.
∴∠E=∠BCP,
∴∠BCP+∠BCE=90°,即∠PCE=90°,
∴CE⊥PC,
∴PC与圆O相切;
(2)∵AD是⊙O的切线,切点为A,
∴OA⊥AD,
∵BC∥AD,
∴AM⊥BC,
∴BM=CM=
BC=3,
∴AC=AB=9,
在Rt△AMC中,AM=
=6
,
设⊙O的半径为r,则OC=r,OM=AM-r=6
-r,
在Rt△OCM中,OM2+CM2=OC2,即32+(6
-r)2=r2,解得r=
,
∴CE=2r=
,OM=6
-
=
,
∴BE=2OM=
,
∵∠E=∠MCP,
∴Rt△PCM∽Rt△CEB,
∴
=
,
即
=
,
∴PC=
.
 解:(1)PC与圆O相切,理由为:
解:(1)PC与圆O相切,理由为:过C点作直径CE,连接EB,如图,
∵CE为直径,
∴∠EBC=90°,即∠E+∠BCE=90°,
∵AB∥DC,
∴∠ACD=∠BAC,
∵∠BAC=∠E,∠BCP=∠ACD.
∴∠E=∠BCP,
∴∠BCP+∠BCE=90°,即∠PCE=90°,
∴CE⊥PC,
∴PC与圆O相切;
(2)∵AD是⊙O的切线,切点为A,
∴OA⊥AD,
∵BC∥AD,
∴AM⊥BC,
∴BM=CM=
| 1 |
| 2 |
∴AC=AB=9,
在Rt△AMC中,AM=
| AC2-CM2 |
| 2 |
设⊙O的半径为r,则OC=r,OM=AM-r=6
| 2 |
在Rt△OCM中,OM2+CM2=OC2,即32+(6
| 2 |
27
| ||
| 8 |
∴CE=2r=
27
| ||
| 4 |
| 2 |
27
| ||
| 8 |
21
| ||
| 8 |
∴BE=2OM=
21
| ||
| 4 |
∵∠E=∠MCP,
∴Rt△PCM∽Rt△CEB,
∴
| PC |
| CE |
| CM |
| EB |
即
| PC | ||||
|
| 3 | ||||
|
∴PC=
| 27 |
| 7 |
点评:本题考查了切线的判定与性质:过半径的外端点与半径垂直的直线为圆的切线;圆的切线垂直于过切点的半径.也考查了勾股定理、圆周角定理的推论、三角形相似的判定与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
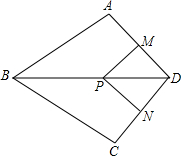 (2013•南京)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(2013•南京)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.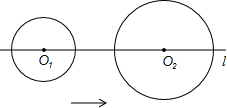 (2013•南京)如图,⊙O1,⊙O2的圆心在直线l上,⊙O1的半径为2cm,⊙O2的半径为3cm.O1O2=8cm,⊙O1以1cm/s的速度沿直线l向右运动,7s后停止运动.在此过程中,⊙O1和⊙O2没有出现的位置关系是( )
(2013•南京)如图,⊙O1,⊙O2的圆心在直线l上,⊙O1的半径为2cm,⊙O2的半径为3cm.O1O2=8cm,⊙O1以1cm/s的速度沿直线l向右运动,7s后停止运动.在此过程中,⊙O1和⊙O2没有出现的位置关系是( ) (2013•南京)如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=
(2013•南京)如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α= (2013•南京)如图,在梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于P.已知A(2,3),B(1,1),D(4,3),则点P的坐标为(
(2013•南京)如图,在梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于P.已知A(2,3),B(1,1),D(4,3),则点P的坐标为(