题目内容
【题目】已知点P为抛物线y=x2+2x﹣3在第一象限内的一个动点，且P关于原点的对称点P′恰好也落在该抛物线上，则点P′的坐标为（ ）
A. （﹣1，﹣1） B. （﹣2，﹣
） C. （﹣
，﹣2﹣1） D. （﹣，﹣2）
【答案】D
【解析】分析：
设点P的坐标为（x，y），则点P′的坐标为（-x，-y），把两个点的坐标代入y=x2+2x﹣3中列出关于x、y的方程组，解方程组结合点P在第一象限即可求得点P的坐标，由此即可得到点P′的坐标了.
详解：
设P点的坐标为（x，y），
∵点P′与点P关于原点对称，
∴点P′的坐标为（﹣x，﹣y），
把点P（x，y）和点P′（﹣x，﹣y）代入y=x2+2x﹣3得：
，解得：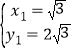
，
，
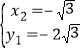∵点P在第一象限，
∴点P的坐标为
，
∴点P′的坐标为
.
故选D．
练习册系列答案
相关题目
