题目内容
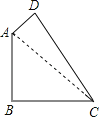
【题目】在△ABC中,AD是它的角平分线.
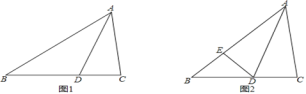
(1)如图1,求证:S△ABD:S△ACD=AB:AC=BD:CD;
(2)如图2,E是AB上的点,连接ED,若BD=3,BE=CD=2,AE=2CD,求证:△BED是等腰三角形;
(3)在图1中,若3∠BAC=2∠C,∠ADB>∠B>∠BAD,直接写出∠BAC的取值范围 .
【答案】(1)证明见解析;(2)证明见解析;(3)40°<∠BAC<60°.
【解析】
(1)作辅助线,构建三角形的性质得:DE=DF,利用三角形面积的不同计算方法可得结论;
(2)证明△AED≌△ACD,可得DE=CD=BE,可得结论;
(3)设∠BAD=x,根据∠ADB>∠B>∠BAD,列不等式可解答.
证明:(1)如图1,过D作DE⊥AB于E,DF⊥AC于F,
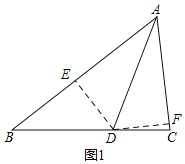
∵AD平分∠BAC,
∴DE=DF,
∴![]() =
=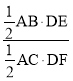 =
=![]() =
=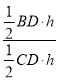 =
=![]() ;
;
S△ABD:S△ACD=AB:AC=BD:CD;
(2)如图2,由(1)知:AB:AC=BD:CD;
∵BE=CD=2,AE=2CD=4,
∴![]() ,AC=4=AE,
,AC=4=AE,
在△AED和△ACD中
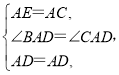
∴△AED≌△ACD(SAS),
∴ED=CD=2,
∵BE=2,∴BE=DE=2,
∴△BED是等腰三角形;
(3)设∠BAD=x,则∠BAC=2x,
∵3∠BAC=2∠C,
∴∠C=3x,
∴∠ADB=∠DAC+∠C=4x,
∵∠ADB>∠B>∠BAD,
∴4x>1805x>x,
解得:20°<x<30°,
∴40°<∠BAC<60°.
故答案为:40°<∠BAC<60°.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案
相关题目