Question

【题目】如图，将带有45°和30°两块直角三角尺的直角顶点C叠放在一起，

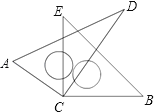
（1）若∠DCE＝25°，则∠ACB＝______；若∠ACB＝150°，则∠DCE＝______；

（2）猜想∠ACB与∠DCE的大小有何特殊关系，并说明理由．

Answer 1

【答案】（1）155°；30°；（2）∠ACB+∠DCE＝180°，理由见解析.

【解析】

（1）由∠ACD＝90°，∠DCE＝25°，得出∠ACE＝65°，求出∠ACB＝∠ACE+∠BCE＝155°；若∠ACB＝150°，由∠ACD＝∠BCE＝90°，得出∠DCE＝180°﹣150°＝30°；

（2）由∠ACD＝∠BCE＝90°，得出∠ACE+∠DCE+∠DCE+∠BCD＝180°，结合已知条件，即可得出结论．

（1）∵∠ACD＝90°，∠DCE＝25°，

∴∠ACE＝90°﹣25°＝65°，

∵∠BCE＝90°，

∴∠ACB＝∠ACE+∠BCE＝65°+90°＝155°；

故答案为：155°

∵∠ACB＝150°，∠ACD＝∠BCE＝90°，

∴∠DCE＝90°+90°﹣∠ACB＝180°﹣150°＝30°；

故答案为：30°

（2）∠ACB+∠DCE＝180°．理由如下：

∵∠ACD＝∠BCE＝90°，

∴∠ACE+∠DCE+∠DCE+∠BCD＝180°，

∵∠ACE+∠DCE+∠BCD=∠ACB，

∴∠ACB+∠DCE＝180°．