题目内容
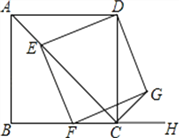
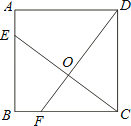
【题目】如图1和2,四边形ABCD是菱形,点P是对角线AC上一点,以点P为圆心,PB为半径的弧,交BC的延长线于点F,连接PF,PD,PB.
(1)如图1,点P是AC的中点,请写出PF和PD的数量关系:;
(2)如图2,点P不是AC的中点,
①求证:PF=PD.
②若∠ABC=40°,直接写出∠DPF的度数.
【答案】
(1)PF=PD
(2)
解:①证明:
∵四边形ABCD是菱形,
∴AB=AD,∠BAC=∠DAC.
在△ABP和△ADP中,
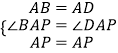 ,
,
∴△ABP≌△ADP(SAS),
∴PB=PD,
又∵PB=PF,
∴PF=PD.
②解:以P为圆心,PB为半径作圆P,则点B、F、D都在圆P上,连接BD.
由圆周角定理,可得∠DPF=2∠DBF,
又∵四边形ABCD是菱形,
∴∠ABC=2∠DBF,
∴∠DPF=∠ABC=40°.
【解析】(1)先根据菱形的对角线互相平分得出PB=PD,而由已知有PB=PF,则PF=PD;(2)①先由菱形的性质得出AB=AD,∠BAC=∠DAC,再由SAS证明△ABP≌△ADP,得出PB=PD,又PB=PF,则PF=PD;
②由于PB=PD=PF,以P为圆心,PB为半径作圆P,则点B、F、D都在圆P上,连接BD,则∠DPF=2∠DBF=∠ABC=40°.
【考点精析】本题主要考查了菱形的性质的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.

练习册系列答案
相关题目