��Ŀ����
����Ŀ���ס�����У�μ���ѧ��������У�μӳ�����������ȣ�������������ѧ���ɼ��ֱ�Ϊ 70 �֡�80 �֡�90 �֡�100 �֣�����ͳ�����ݻ����������в�������ͳ��ͼ����
��У�ɼ�ͳ�Ʊ���
���� | 70 �� | 80 �� | 90 �� | 100 �� |
���� | 11 | 0 | 8 |

(1)��ͼ 1 �У���80 �������ڵ����ε�Բ�Ľǵ��� �ȣ�
(2)�뽫��У�ɼ�ͳ�Ʊ���ͼ 2 ����У�ɼ�����ͳ��ͼ����������
(3)������У��ƽ���ֺͼ�У����λ����
(4)����ؽ�����Ҫ��֯ 8 �˵Ĵ����Ӳμ��м�����������������Ϊ�˱��ڹ�����������������ѧУ�е�һ����ѡ����ѡ�֣�����ΪӦѡ�ĸ�ѧУ�����Ҫ˵�����ɣ�
���𰸡���1��54������2����������3����У��ƽ����Ϊ83�֣� ��У��λ��Ϊ70����4��ѡ��У�����ɼ�����
��������
��1����������ͳ��ͼ�������Բ�ĽǶ����������;
��2��������У�μӳ�����������������У90�ֵ����������ɲ�ȫ��У�ɼ�ͳ�Ʊ���У�ɼ�����ͳ��ͼ��
��3�����ݼ�Ȩƽ�����Ķ�������λ���Ķ��弴����⣻
��4���۲���У�ĸ߷��������з�������.
��1����80 �������ڵ����ε�Բ�Ľǵ���360��-90��-72��-144��=54����
��2��5��25%=20���ˣ�20��![]() =3���ˣ�
=3���ˣ�
��У90�ֵ�������20-11-8=1�ˣ�
��ȫ������ͳ��ͼ���£�
���� | 70 �� | 80 �� | 90 �� | 100 �� |
���� | 11 | 0 | 1 | 8 |
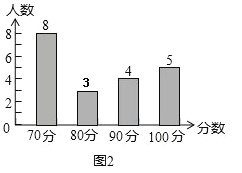
��3����У��ƽ����Ϊ��70��8+80��3+90��4+100��5����20=83��
��У��10,11���ķ���Ϊ70,70������λ��Ϊ70��
��4����У100�ֵ�����Ϊ8�ˣ���У100�ֵ�����Ϊ5�ˣ�
��ѡ��У.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij���ӳ��������һ������ɱ�Ϊ18Ԫ���͵��ӳ�Ʒ��Ͷ���г������������������飬�õ�ÿ��������y������������۵���x��Ԫ��֮��IJ����������£�
���۵���x��Ԫ/���� | �� | 20 | 25 | 30 | 35 | �� |
ÿ��������y������� | �� | 60 | 50 | 40 | 30 | �� |
��1�����ÿ��������y������������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2�����ÿ�µ�����z����Ԫ�������۵�x��Ԫ��֮��ĺ�����ϵʽ��
��3��������ز��Ź涨�����ֵ��Ӳ�Ʒ�����������ʲ��ܸ���50%�����Ҹõ��ӳ���������ֲ�Ʒÿ�µ�����ɱ����ܳ���900��Ԫ����ô����������۵��۶�Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�������=�ۼ۩�����ɱ���