题目内容
【题目】某班“数学兴趣小组”对函数y=x![]() 2|x|的图象和性质进行了探究,探究过程如下,请补充完整:
2|x|的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
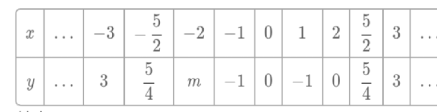
其中,m=___.
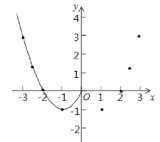
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)探究函数图象发现:
①函数图象与x轴有___个交点,所以对应的方程x![]() 2|x|=0有___个实数根;
2|x|=0有___个实数根;
②方程x![]() 2|x|=
2|x|=![]() 有___个实数根;
有___个实数根;
③关于x的方程x![]() 2|x|=a有4个实数根时,a的取值范围是___.
2|x|=a有4个实数根时,a的取值范围是___.
【答案】(1)0;(2)见解析;(3)①3、3;②4;③0<a<1.
【解析】
(1)根据当x=2或x=-2时函数值相等即可得;
(2)将坐标系中y轴左侧的点按照从左到右的顺序用平滑的曲线依次连接可得;
(3)①根据函数图象与x轴的交点个数与对应方程的解的个数间的关系可得;
②由直线y=-![]() 与y=x
与y=x![]() -2|x|的图象有4个交点可得;
-2|x|的图象有4个交点可得;
③关于x的方程x![]() -2|x|=a有4个实数根时,0<a<-1.
-2|x|=a有4个实数根时,0<a<-1.
(1)由函数解析式y=x![]() 2|x|知,当x=2或x=2时函数值相等,
2|x|知,当x=2或x=2时函数值相等,
∴当x=2时,m=0,
故答案为:0;
(2)如图所示:
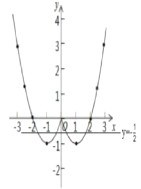
(3)①由图象可知,函数图象与x轴有3个交点,所以对应的方程x![]() 2|x|=0有3个实数根;
2|x|=0有3个实数根;
②由函数图象知,直线y=![]() 与y=x
与y=x![]() 2|x|的图象有4个交点,
2|x|的图象有4个交点,
所以方程x![]() 2|x|=
2|x|=![]() 有4个实数根;
有4个实数根;
③由函数图象知,关于x的方程x![]() 2|x|=a有4个实数根时,0<a<1,
2|x|=a有4个实数根时,0<a<1,
故答案为:0<a<1;
故答案为:①3、3;②4;③0<a<1.

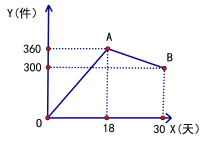
【题目】甲、乙两校参加数学竞赛,两校参加初赛的人数相等.初赛结束后,发现学生成绩分别为 70 分、80 分、90 分、100 分.依据统计数据绘制了如下尚不完整的统计图表.
甲校成绩统计表:
分数 | 70 分 | 80 分 | 90 分 | 100 分 |
人数 | 11 | 0 | 8 |

(1)在图 1 中,“80 分”所在的扇形的圆心角等于 度;
(2)请将甲校成绩统计表和图 2 的乙校成绩条形统计图补充完整;
(3)计算乙校的平均分和甲校的中位数;
(4)如果县教育局要组织 8 人的代表队参加市级复赛(团体赛),为了便于管理,决定从这两所学校中的一所挑选参赛选手,你认为应选哪个学校?请简要说明理由.