Question

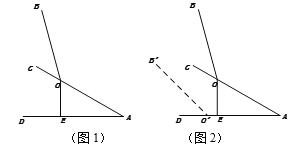
【题目】小林在使用笔记本电脑时，为了散热，他将电脑放在散热架CAD上，忽略散热架和电脑的厚度，侧面示意图如图1所示，已知电脑显示屏OB与底板OA的夹角为135°，OB=OA=25cm，OE⊥AD于点E，OE=12.5cm.

（1）求∠OAE的度数；

（2）若保持显示屏OB与底板OA的135°夹角不变，将电脑平放在桌面上如图2中的所示，则显示屏顶部比原来顶部B大约下降了多少？(参考数据：结果精确到0.1cm.参考数据：sin75°≈0.97，cos75°≈0.26，tan75°≈3.73，，)

Answer 1

【答案】（1）∠OAE=30°；（2）19.1cm

【解析】

（1）根据题中数据，在△OEA中，将∠OAE的正弦值求出，从而得出∠OAE的度数.

（2）过点O作MN⊥OE，过点B作BH⊥MN于点H，过点B＇作B＇F⊥AD，交AD的延长线于点F. 通过∠BOH的度数，计算出BH的长度，在△B＇O＇F中，求出∠B＇O＇F的度数，从而求出B＇F的长度，利用OE和BH的长度之和得出B点距离桌面的高度，最后求出下降的高度.

解：（1）∵OE⊥AD于点E，OA=OB=25cm，OE=12.5cm，

在Rt△OEA中，.

∴∠OAE=30°.

（2）如图，过点O作MN⊥OE，过点B作BH⊥MN于点H，过点B＇作B＇F⊥AD，交AD的延长线于点F.

∵∠BOA=135°，∠AOE=60°，∠MOE=90°

∴∠BOH=360°－∠BOA －∠AOE －∠MOE =75°

∵在Rt△BOH中，

∴

=25×sin75°≈25×0.97=24.25（cm）

∵=135°

∴=45°

∵在Rt△中，

∴=25×≈25×0.705=17.625（cm）

∴BH+OE－B＇F≈24.25+12.5－17.625=19.125≈19.1（cm）

答：显示屏顶部比原来顶部B大约下降了19.1cm.