Question

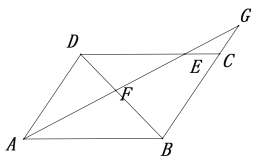
【题目】如图，在平行四边形ABCD中，点E为边DC上一点，且DE∶EC=3∶1，连接AE并延长，与BC的延长线交于点G，AE与BD交于点F，则△GEC的面积与△DEF的面积之比为（ ）

A.1∶3B.3∶7C.4∶21D.7∶27

Answer 1

【答案】D

【解析】

通过△DFE和△BFA的相似比得出△DFE和△DEA的高的比，继而得出面积之比，再通过△ADE和△GCE的相似比得出面积比，从而得出△GCE和△DEF的面积之比.

解：由题意可知，在平行四边形ABCD中，△DFE∽△BFA，△ADE∽△GCE，

∵DE∶EC=3∶1，CD=AB，

∴△DFE和△BFA的相似比为3∶4，

∴△DFE和△BFA的高的比为3∶4，

∴△DFE和△DEA的面积比为3∶7，

∵△ADE∽△GCE，EC∶CD =1∶4,

∴△ADE和△GCE的面积比为9∶1，

∴△GCE和△DEF的面积比为：7∶27.

故选D.