Question

【题目】在平行四边形ABCD中，点E是AD边上的点，连接BE．

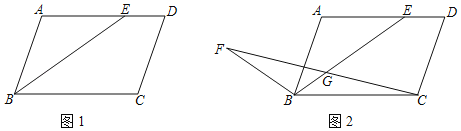
（1）如图1，若BE平分∠ABC，BC＝8，ED＝3，求平行四边形ABCD的周长；

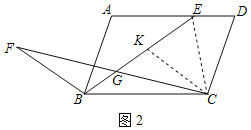
（2）如图2，点F是平行四边形外一点，FB＝CD．连接BF、CF，CF与BE相交于点G，若∠FBE+∠ABC＝180°，点G是CF的中点，求证：2BG+ED＝BC．

Answer 1

【答案】（1）26；（2）见解析

【解析】

（1）由平行四边形的性质得出AD＝BC＝8，AB＝CD，AD∥BC，由平行线的性质得出∠AEB＝∠CBE，由BE平分∠ABC，得出∠ABE＝∠CBE，推出∠ABE＝∠AEB，则AB＝AE，AE＝AD﹣ED＝BC﹣ED＝5，得出AB＝5，即可得出结果；

（2）连接CE，过点C作CK∥BF交BE于K，则∠FBG＝∠CKG，由点G是CF的中点，得出FG＝CG，由AAS证得△FBG≌△CKG，得出BG＝KG，CK＝BF＝CD，由平行四边形的性质得出∠ABC＝∠D，∠BAE+∠D＝180°，AB＝CD＝CK，AD∥BC，由平行线的性质得出∠DEC＝∠BCE，∠AEB＝∠KBC，易证∠EKC＝∠D，∠CKB＝∠BAE，由AAS证得△AEB≌△KBC，得出BC＝BE，则∠KEC＝∠BCE，推出∠KEC＝∠DEC，由AAS证得△KEC≌△DEC，得出KE＝ED，即可得出结论．

（1）∵四边形ABCD是平行四边形，

∴AD＝BC＝8，AB＝CD，AD∥BC，

∴∠AEB＝∠CBE，

∵BE平分∠ABC，

∴∠ABE＝∠CBE，

∴∠ABE＝∠AEB，

∴AB＝AE，

∵AE＝AD﹣ED＝BC﹣ED＝8﹣3＝5，

∴AB＝5，

∴平行四边形ABCD的周长＝2AB+2BC＝2×5+2×8＝26；

（2）连接CE，过点C作CK∥BF交BE于K，如图2所示：

则∠FBG＝∠CKG，

∵点G是CF的中点，

∴FG＝CG，

在△FBG和△CKG中，

∵ ，

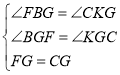∴△FBG≌△CKG（AAS），

∴BG＝KG，CK＝BF＝CD，

∵四边形ABCD是平行四边形，

∴∠ABC＝∠D，∠BAE+∠D＝180°，AB＝CD＝CK，AD∥BC，

∴∠DEC＝∠BCE，∠AEB＝∠KBC，

∵∠FBE+∠ABC＝180°，

∴∠FBE+∠D＝180°，

∴∠CKB+∠D＝180°，

∴∠EKC＝∠D，

∵∠BAE+∠D＝180°，

∴∠CKB＝∠BAE，

在△AEB和△KBC中，

∵，

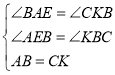∴△AEB≌△KBC（AAS），

∴BC＝EB，

∴∠KEC＝∠BCE，

∴∠KEC＝∠DEC，

在△KEC和△DEC中，

∵，

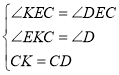∴△KEC≌△DEC（AAS），

∴KE＝ED，

∵BE＝BG+KG+KE＝2BG+ED，

∴2BG+ED＝BC．