题目内容
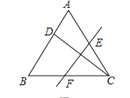
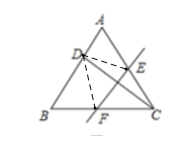
【题目】如图,已知D是等边△ABC边AB上的一点,现将△ABC折叠,使点C与D重合,折痕为EF,点E、F分别在AC和BC上.如果AD:DB=1:2,则CE:CF的值为____________.
【答案】![]()
【解析】
根据折叠的性质可得DE=CE,DF=CF,利用两角对应相等的两三角形相似得出△AED∽△BDF,进而得出对应边成比例得出比例式,将比例式变形即可得.
解:如图,连接DE,DF,
∵△ABC是等边三角形,
∴AB=BC=AC, ∠A=∠B=∠ACB=60°,
由折叠可得,∠EDF=∠ACB=60°,DE=CE,DF=CF
∵∠BDE=∠BDF+∠FDE=∠A+∠AED,
∴∠BDF+60°=∠AED+60°,
∴∠BDF=∠AED,
∵∠A=∠B,
∴△AED∽△BDF,
∴![]() ,
,
设AD=x,∵AD:DB=1:2,则BD=2x,
∴AC=BC=3x,
∵![]() ,
,
∴![]()
∴![]()
∴![]() ,
,
∴![]() .
.
故答案为:![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】在一个不透明的布袋中,有三个除颜色外其它均相同的小球,其中两个黑色,一个红色.
(1)请用表格或树状图求出:一次随机取出2个小球,颜色不同的概率.
(2)如果老师在布袋中加入若干个红色小球.然后小明通过做实验的方式猜测加入的小球数,小 明每次換出一个小球记录下慎色并放回,实验数据如下表:
实验次数 | 100 | 200 | 300 | 400 | 500 | 1000 |
摸出红球 | 78 | 147 | 228 | 304 | 373 | 752 |
请你帮小明算出老师放入了多少个红色小球.
【题目】学校为了解九年级学生对“八礼四仪”的掌握情况,对该年级的500名同学进行问卷测试,并随机抽取了10名同学的问卷,统计成绩如下:
得分 | 10 | 9 | 8 | 7 | 6 |
人数 | 3 | 3 | 2 | 1 | 1 |
(1)计算这10名同学这次测试的平均得分;
(2)如果得分不少于9分的定义为“优秀”,估计这 500名学生对“八礼四仪”掌握情况优秀的人数;
(3)小明所在班级共有40人,他们全部参加了这次测试,平均分为7.8分.小明的测试成绩是8分,小明说,我的测试成绩在班级中等偏上,你同意他的观点吗?为什么?