Question

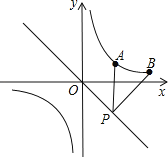
【题目】如图，在反比例函数y=上有两点A（3，2），B（6，1），在直线y=﹣x上有一动点P，当P点的坐标为 时，PA+PB有最小值．

Answer 1

【答案】（，﹣）．

【解析】

试题分析：设A点关于直线y=﹣x的对称点为A′，连接A′B，交直线y=﹣x为P点，此时PA+PB有最小值，求出直线A′B的直线解析式，再与y=﹣x联立，求出交点坐标，P点坐标即可求出．

解：设A点关于直线y=﹣x的对称点为A′，连接A′B，交直线y=﹣x为P点，此时PA+PB有最小值，

∵A点关于直线y=﹣x的对称点为A′，A（3，2），

∴A′（﹣2，﹣3），

设直线A′B的直线解析式为y=kx+b，

，

解得k=，b=﹣2，

∴直线A′B的直线解析式为y=x﹣2，

联立，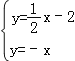

解得x=，y=﹣，

即P点坐标（，﹣），

故答案为（，﹣）．