题目内容
【题目】如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,下列结论:①∠ACD=∠B;②CH=CE=EF;③AC=AF;④CH=HD.其中正确的结论为( )
A.①②④ B.①②③ C. ②③ D.①③
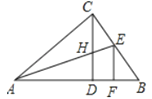
【答案】B
【解析】
试题分析:根据等角的余角相等可判断①;先判断CD∥EF,根据平行线的性质得出∠CEH=∠CHE,再由角平分线的性质可判断②;用AAS判定△ACE≌△AFE,可判断③;根据②,结合图形可判断④.
∵∠B和∠ACD都是∠CAB的余角,∴∠ACD=∠B,故①正确;
∵CD⊥AB,EF⊥AB,∴EF∥CD,∴∠AEF=∠CHE,∴∠CEH=∠CHE,∴CH=CE=EF,故②正确;
∵角平分线AE交CD于H,∴∠CAE=∠BAE,∴△ACE≌△AFE(AAS),∴AC=AF,故③正确;
CH=CE=EF>HD,故④错误.

练习册系列答案
相关题目