题目内容
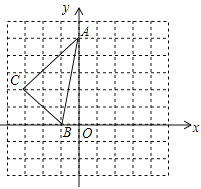
【题目】如图所示,某船上午11时30分在A处观测海岛B在北偏东60°方向,该船以每小时10海里的速度航行到C处,再观测海岛B在北偏东30°方向,又以同样的速度继续航行到D处,再观测海岛在北偏西30°方向,当轮船到达C处时恰好与海岛B相距20海里,请你确定轮船到达C处和D处的时间.

【答案】轮船到达C处的时间为13时30分,到达D处的时间15时30分
【解析】
试题分析:首先根据题意得出∠BAC=30°,∠BCD=60°,从而得出∠BAC=∠CBA=30°,则AC=BC,根据题意得出∠BDC=60°,得到△BCD为等边三角形,则BC=AC=CD=BD=20,从而求出船从A点到达C点所用的时间和船从C点到达D点所用的时间.
试题解析:∵在A处观测海岛B在北偏东60°方向,∴∠BAC=30°,
∵C点观测海岛B在北偏东30°方向,∴∠BCD=60°, ∴∠BAC=∠CBA=30°,∴AC=BC.
∵D点观测海岛在北偏西30°方向 ∴∠BDC=60° ∴∠BCD=60° ∴∠CBD=60° ∴△BCD为等边三角形,
∴BC=BD,∵BC=20,∴BC=AC=CD=20,
∵船以每小时10海里的速度从A点航行到C处,又以同样的速度继续航行到D处,
∴船从A点到达C点所用的时间为:20÷10=2(小时),
船从C点到达D点所用的时间为:20÷10=2(小时),
∵船上午11时30分在A处出发,D点观测海岛B在北偏西30°方向,
∴到达D点的时间为13时30分+2小时=15时30分.
答:轮船到达C处的时间为13时30分,到达D处的时间15时30分.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目