Question

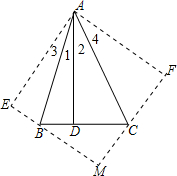
在△ABC中，∠BAC=45°，AD⊥BC于D，将△ABD沿AB所在的直线折叠，使点D落在点E处；将△ACD沿AC所在的直线折叠，使点D落在点F处，分别延长EB、FC使其交于点M．
（1）判断四边形AEMF的形状，并给予证明；
（2）若BD=1，CD=2，试求四边形AEMF的面积．

Answer 1

（1）∵AD⊥BC，
△AEB是由△ADB折叠所得，
∴∠1=∠3，∠E=∠ADB=90°，BE=BD，AE=AD．
又∵△AFC是由△ADC折叠所得，
∴∠2=∠4，∠F=∠ADC=90°，FC=CD，AF=AD．
∴AE=AF．（2分）
又∵∠1+∠2=45°，
∴∠3+∠4=45°．
∴∠EAF=90°．（3分）
∴四边形AEMF是正方形．（5分）

（2）方法一：设正方形AEMF的边长为x；
根据题意知：BE=BD，CF=CD，
∴BM=x-1；CM=x-2．（7分）
在Rt△BMC中，由勾股定理得：BC²=CM²+BM²
∴（x-1）²+（x-2）²=9，
x²-3x-2=0，
解之得：x1=

3+ 17

2

x2=

3- 17

2

（舍去）．
∴S正方形AEMF=(

3+ 17

2

)2=

13+3 17

2

．（10分）
方法二：设：AD=x
∴S△ABC=

1

2

•BC•AD=

3

2

x
∴S_{五边形AEBCF}=2S_△ABC=3x（7分）
∵S△BMC=

1

2

BM•CM=

1

2

(x-1)(x-2)
且S_{正方形AEMF}=S_{五边形AEBCF}+S_△BMC，
∴x2=3x+

1

2

(x-1)(x-2)即x²-3x-2=0，
解之得：x1=

3+ 17

2

，x2=

3- 17

2

（舍去），
∴S正方形AEMF=(

3+ 17

2

)2=

13+3 17

2

．（10分）