题目内容
如图,若AB是⊙0的直径,CD是⊙O的弦,∠ABD=58°, 则∠BCD=( )
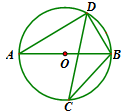

| A.116° | B.32° |
| C.58° | D.64° |
B.
试题分析:根据AB是⊙0的直径,利用直径所对的圆周角是直角,求出∠ADB=90°,然后利用三角形的内角和定理,求出∠A的度数,最后根据同圆中,同弧或等弧所对的圆周角相等,证明∠C=∠A,从而求出∠BCD的度数.
∵AB是⊙0的直径,∴∠ADB=90°.
∵∠A+∠ABD+∠ADB=180°,∠ABD=58°,
∴∠A=180°-58°-90°=32°.
∴∠BCD=∠A=32°.
故选择B.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 垂直于弦
垂直于弦 ,垂足为
,垂足为 ,若
,若 ,
, ,则
,则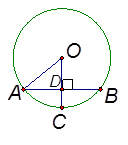

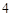




 cm
cm