题目内容
【题目】如图,在平行四边形ABCD和平行四边形AECF的顶点,D,E,F,B在一条直线上,则下列等式成立的是( )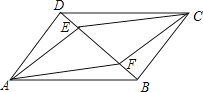
A.AE=CE
B.CE=CF
C.DE=BF
D.DE=EF=BF
【答案】C
【解析】
平行四边形的对比平行且相等,所以AB=DC,AD=BC,所以∠ABD=∠CDF,∠AEB=∠CFD,所以易证△AEB≌△CFD,故各个结论可证.
∵四边形AECF是平行四边形
∴AE=CF,CE=AF(∴A、B不成立)
∵在平行四边形AECF和平行四边形ABCD中,AE∥CF,AB∥CD
∴∠ABD=∠CDF,∠AEB=∠CFD
∵AB=CD
∴△AEB≌△CFD
∴DF=BE
∴DE=BF(∴C成立,D不成立)
故选C.
【考点精析】关于本题考查的平行四边形的性质,需要了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能得出正确答案.

练习册系列答案
相关题目