题目内容
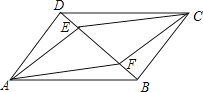
【题目】如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF．求证：四边形DEBF是平行四边形．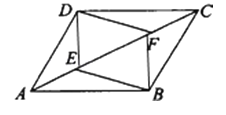
【答案】证明：连接BD，交AC于点O，
∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∵AE=CF，
∴OA﹣AE=OC﹣CF，
即OE=OF，
∴四边形DEBF是平行四边形．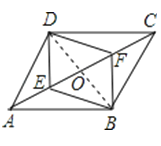
【解析】首先连接BD，交AC于点O，由四边形ABCD是平行四边形，根据平行四边形的对角线互相平分，即可求得OA=OC，OB=OD，又由AE=CF，可得OE=OF，然后根据对角线互相相平分的四边形是平行四边形．
【考点精析】本题主要考查了全等三角形的性质和平行四边形的判定与性质的相关知识点，需要掌握全等三角形的对应边相等; 全等三角形的对应角相等；若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积才能正确解答此题．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，把超过或不足的部分分别用正、负数来表示，记录如下表：
与标准质量的差值（单位：克） | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
（1）若每袋食品的标准质量为450克，则抽样检测的20袋食品的总质量是多少克？
（2）若该种食品的合格标准为450±5克，求该种食品抽样检测的合格率？
