题目内容
【题目】如图,两建筑物AB、CD的水平距离BC为60m,从A点测得D点的俯角α为30°,测得C点的俯角β为45°,求建筑物AB、CD的高度.(结果保留根号)
【答案】解:过点D作DE⊥AB于点E,则四边形BCDE是矩形,
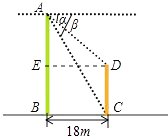
由题意得,∠ACB=β=60°,∠ADE=α=30°,BC=60m,
∴DE=BC=60m,CD=BE,
在Rt△ABC中,AB=BCtan∠ACB=60×tan60°=60 ![]() (m),
(m),
在Rt△ADE中,AE=DEtan∠ADE=60×tan30°=20 ![]() (m),
(m),
∴CD=BE=AB﹣AE=60 ![]() ﹣20
﹣20 ![]() (m).
(m).
答:建筑物AB、CD的高度分别为60 ![]() m、20
m、20 ![]() m.
m.
【解析】过点D作DE⊥AB于点E,则四边形BCDE是矩形,由题意得,∠ACB=β=60°,∠ADE=α=30°,BC=60m,由矩形的性质得DE=BC=60m,CD=BE,解直角三角形得出AB,AE的长度,即可。
【考点精析】关于本题考查的关于仰角俯角问题,需要了解仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能得出正确答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




