题目内容
【题目】已知一次函数y=kx+b的图象经过点(0,1),且与正比例函数y=![]() x的图象相交于点(2,a).
x的图象相交于点(2,a).

求:(1)a的值;
(2)一次函数y=kx+b的解析式;
(3)在图中画出这两个函数图象,并求这两个函数图象与x轴所围成的三角形面积.
【答案】(1)a=1;(2)![]() ;(3)画这两个函数图象见解析;面积为
;(3)画这两个函数图象见解析;面积为![]() .
.
【解析】
(1)将点(2,a)代入正比例函数y=![]() x中,即可求出a的值;
x中,即可求出a的值;
(2)将(0,1)和(2,1)分别代入一次函数y=kx+b中,即可求出一次函数的解析式;
(3)利用两点法画出两函数的图像,然后根据三角形的面积公式计算面积即可.
解:(1)将点(2,a)代入正比例函数y=![]() x中,得:a=
x中,得:a=![]() ×2=1;
×2=1;
(2)∵将(0,1)和(2,1)分别代入一次函数y=kx+b中,得
![]()
解得:![]()
∴一次函数的解析式为:![]() ;
;
(3)根据一次函数过点(0,1)和点(2,1),画出![]() 的图像;根据正比例函数过点(0,0)和点(2,1),画出y=
的图像;根据正比例函数过点(0,0)和点(2,1),画出y=![]() x的图像,如图所示,直线
x的图像,如图所示,直线![]() 和直线y=
和直线y=![]() x即为所求.
x即为所求.
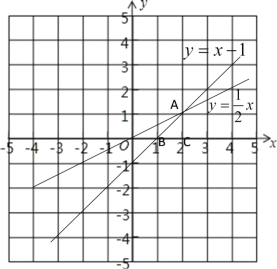
如上图所示,∵点A的坐标为(2,1)
∴AC=1
将y=0代入![]() 中,解得:
中,解得:![]()
∴B点坐标为(1,0)
∴OB=1
∴这两个函数图象与x轴所围成的三角形面积:S△AOB=![]() OB·AC=
OB·AC=![]() .
.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目