Question

【题目】已知关于x的一元二次方程x2-(2k+3)+k2+3k-4=0．

(1) 试判断上述方程根的情况并说明理由；

(2) 若以上一元二次方程的两个根分别为、(),

① m=________,n=_________；

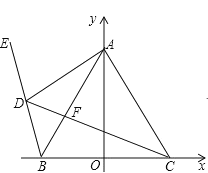
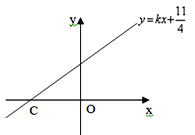
②当时，点A、B分别是直线：y=kx+上两点且A、B两点的横坐标分别为、，直线与轴相交于点C，若S△BOC=2S△AOC，求的值；

（3）在(2)的条件下，问在轴上是否存在点Q，使△ABQ的三个内角平分线交点在轴上？若存在，求出点Q的坐标，若不存在，请说明理由．

Answer 1

【答案】(1)方程有两个不相等的实数根，理由略；(2)①m=k-1 n=k+4；② k=；(3)(0，) .

【解析】

（1）根据判别式的值即可判断；

（2）①根据一元二次方程的求根公式即可得出；

②先根据三角形的面积公式列出关于m，n的式子，再将m= k-1，n= k+4代入，即可得出答案；

（3）假设存在点Q，使△ABQ的三个内角平分线交点在轴上，则此时y轴就是∠AQB的角平分线，从而得知点B（，5）和对称点B'（-，5）在直线AQ上，待定系数法可得直线AQ的解析式，由点Q在y轴上即可得点Q的坐标．

解：（1）∵x2-(2k+3)x+k2+3k-4=0，

∴△=b2-4ac=（2k+3）2-4（k2+3k-4）=4k2+12k+9-4k2-12k+16=25>0，

∴该方程有两个不相等的实数根．

（2）①∵一元二次方程的求根公式x=，

∴m= = ==k-1，

n====k+4．

② ∵S△BOC=2S△AOC，

S△BOC=××（），

S△AOC=××（），

∴××（）×2=××（），

∴2（）=，

2km-kn=-，

将m= k-1，n= k+4代入，得：2k（k-1）-k（k+4）+=0，

解得：k=或，

∵0<k<1，

∴k=．

（3）由（2）得知，直线l：，A（，），B（，5），

假设存在点Q，使△ABQ的三个内角平分线交点在轴上，则此时y轴就是∠AQB的角平分线，

∴B点关于y轴的对称点必在直线AQ上，设为B'，

∵B（，5），

∴B'（-，5）．

∴直线AQ过A（，），B'（-，5）得到AQ的直线方程为：，

∵点Q在y轴上，当x=0时，y=，

∴Q（0，）．