Question

【题目】如图，长方形ABCD在直角坐标系中，边BC在x轴上，B点坐标为（m，0）且m＞0．AB=a，BC=b，且满足b=.

（1）求a，b的值及用m表示出点D的坐标；

（2）连接OA，AC，若△OAC为等腰三角形，求m的值；

（3）△OAC能为直角三角形吗？若能，求出m的值；若不能，说明理由．

Answer 1

【答案】（1）a=6，b=8；D(m+8，6)；(2) m=8或m=2；(3)能，m=

【解析】

（1）根据二次根式的意义，得出a的值，进而求出b，然后得出OC，即可得出结论；

（2）先利用勾股定理表示出OA，OC，求出AC，分三种情况用两边相等建立方程求解即可；

（3）分三种情况用勾股定理建立方程求解即可求出m．

解：（1）∵，

∴，，

∴，

∴.

∴AB=6，BC=8，

∵B点坐标为（m，0），

∴OC=m+8，

∴点D坐标为：（m+8，6）；

（2）如图，连接OA，AC，

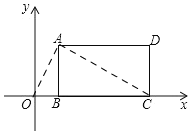
在Rt△ABC中，AB=6，BC=8，根据勾股定理得，AC=10，

在Rt△AOB中，，OC=m+8，

∵△OAC为等腰三角形，

∴①当OA=AC时，

∴，

∴m=8或m=-8（舍去）

②当OA=OC时，

∴，

∴m=（舍去），

③当AC=OC时，

∴10=m+8，

∴m=2，

即：m=2或m=8时，△OAC为等腰三角形；

（3）由（2）知，OA=，OC=m+8，AC=10，

∵△OAC为直角三角形，

∴①当OA2+OC2=AC2时，

∴m2+36+（m+8）2=100，

∴m=0（舍去）或m=-8（舍去）；

②当OA2+AC2=OC2时，

m2+36+100=（m+8）2，

∴m=；

③当AC2+OC2=OA2时，

100+（m+8）2=m2+36，

∴m=-8（舍去），

即：m=时，△OAC为直角三角形．