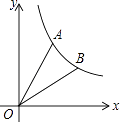题目内容
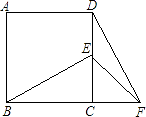
【题目】如图①，抛物线y=ax2+bx+c与x轴正半轴交于A、B两点，与y轴交于点C，直线y=﹣x+2经过A、C两点，且AB=2．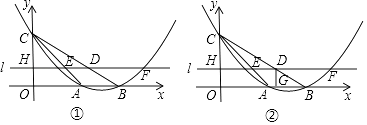
（1）求抛物线的解析式；
（2）若直线l平行于x轴，直线l从点C出发以每秒1个单位长度的速度沿y轴负半轴方向向点O运动，到点O停止，且分别交线段AC、线段BC、抛物线、y轴于点E、D、F（点F在对称轴的右侧）、H，当点D是线段EF的三等分点时，求t的值；
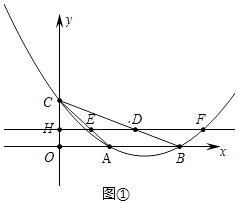
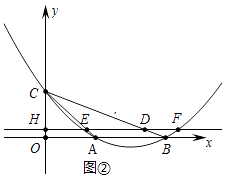
（3）如图②，在直线l运动的过程中，过点D作x轴的垂线交x轴于点G，四边形OHDG与△AOC重叠部分的面积为S，求S与t的函数关系式．
【答案】
（1）
解：∵直线y=﹣x+2与x轴、y轴的交点为A（2，0），C（0，2），AB=2，
∴B（4，0），
把A（2，0）、B（4，0）、C（0，2）代入y=ax2+bx+c中，
得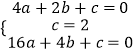 
，解得 
，
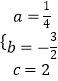∴抛物线的解析式为y= 
x2﹣ 
x+2
（2）
解：∵OA=OC=2，
∴△AOC是等腰直角三角形，
∵直线l∥x轴，
∴△HEC是等腰直角三角形，
∵OA=AB=2，
∴HE=DE，
① 如图①中，当DF=2DE时，点F坐标（4t，2﹣t），
∴2﹣t= ×（4t）2﹣ ×4t+2，
∴t= 
或0（舍弃），
②如图2中，当DE=2DF时，点F坐标（ 
t，2﹣t），
∴2﹣t= ×（ t）2﹣ × t+2，
∴t= 
或0（舍弃），
综上所述，当点D是线段EF的三等分点时，t的值为 s或 s
（3）
解：①如图③当0＜t≤1时，重叠部分是五边形EHOGK，
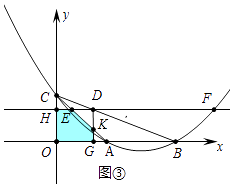
S=S矩形OHDG﹣S△DEK=2t（2﹣t）﹣ 
t2=﹣ t2+4t，
②如图④中，当1＜t＜2时，重叠部分是四边形OHEA，
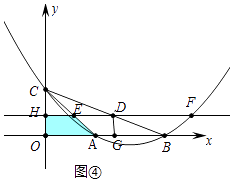
S= （t+2）（2﹣t）=﹣ t2+2，
综上所述，S= 
．
【解析】（1）求出A、B、C三点坐标，代入抛物线的解析式，解方程组即可．（2）分两种情形①如图①中，当DF=2DE时，点F坐标（4t，2﹣t），②如图2中，当DE=2DF时，点F坐标（ t，2﹣t），想办法列出方程解决问题．（3）分两种情形①如图③当0＜t≤1时，重叠部分是五边形EHOGK，②如图④中，当1＜t＜2时，重叠部分是四边形OHEA，分别计算即可．
【考点精析】通过灵活运用求根公式和相似三角形的性质，掌握根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根；对应角相等，对应边成比例的两个三角形叫做相似三角形即可以解答此题．
