Question

【题目】如图，⊙O的半径OB=1，弦AC=1，点D在⊙O上，则∠D的度数是（ ）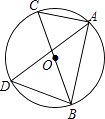
A.60°
B.45°
C.75°
D.30°

Answer 1

【答案】A
【解析】解：∵⊙O的半径OB=1， ∴直径BC=2×1=2，
∵∠BAC是直径BC所对的圆周角，
∴∠BAC=90°，
∵AC=1，
∴BC=2AC，
∴∠ABC=30°，
∴∠C=90°﹣30°=60°，
∵点D在⊙O上，∠C、∠D都是 所对的圆周角，
∴∠D=∠C=60°．
故选A．
求出圆的直径BC的长，然后根据直径所对的圆周角是直角求出∠BAC=90°，然后根据直角三角形30°角所对的直角边等于斜边的一半求出∠ABC=30°，再求出∠C=60°，最后根据在同圆或等圆中，同弧所对的圆周角相等可得∠D=∠C．