题目内容
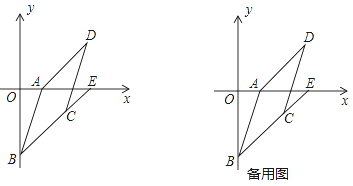
【题目】如图,在平面直角坐标系中,A(a,0),D(6,4),将线段AD平移得到BC,使B(0,b),且a,b满足|a﹣2|+![]() =0,延长BC交x轴于点E.
=0,延长BC交x轴于点E.
(1)填空:点A( , ),点B( , ),∠DAE= ;
(2)求点C和点E的坐标;
(3)设点P是x轴上的一动点(不与点A、E重合),且PA>AE,探究∠APC与∠PCB的数量关系?写出你的结论并证明.
【答案】(1)2,0,0,﹣5,45°;(2)C(4,﹣1),E(5,0)(3)45°或135°
【解析】
(1)根据非负数的性质求出A、B两点的坐标,根据tan∠DAE=1,得出∠DAE=45°;(2)利用平移的性质求出C点坐标,根据待定系数法求出直线BC的解析式,进而得到点E的坐标;(3)分两种情况讨论求解即可解决问题.
(1)∵a,b满足|a﹣2|+![]() =0,
=0,
∴a﹣2=0,b+5=0,
∴a=2,b=﹣5,
∴A(2,0),B(0,﹣5);
∵tan∠DAE=![]() =1,
=1,
∴∠DAE=45°,
故答案为2,0,0,﹣5,45°;
(2)∵AD∥BC,AD=BC,
∴点B先向右平移4个单位再向上平移4个单位得到点C,
∵B(0,﹣5),
∴C(4,﹣1).
∴直线BC的解析式为y=x﹣5,
∴E(5,0).
(3)①当点P在点A的左侧时,如图1,连接PC.
∵OE=OB,
∴∠PEC=45°,
∵∠PCB=∠APC+∠PEC,
∴∠PCB﹣∠APC=45°;
②当P在直线BC与x轴交点的右侧时,如图2,连接PC.
∵∠PCB=∠PEC+∠APC,
∴∠PCB﹣∠APC=135°.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目