题目内容
【题目】在△ABC中∠B=45°,∠C=30°,点D为BC边上任意一点,连接AD,将线段AD绕A顺时针旋转90°,得到线段AE,连接DE.

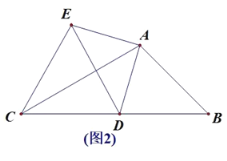
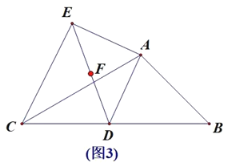
(1)如图1,点E落在BA的延长线上时,∠EDC= (度)直接填空.
(2)如图2,点D在运动过程中,DE⊥AC时,AB=4 ,求DE的值.
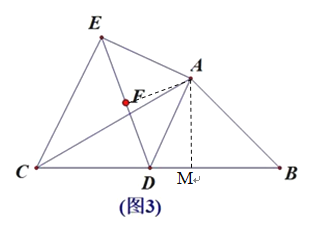
(3)如图3,点F为线段DE中点,AB=![]() ,求出动点D从B运动到C,点F经过的路径长度.
,求出动点D从B运动到C,点F经过的路径长度.
【答案】(1)90°;(2)DE=![]() ;(3)
;(3)![]()
【解析】
(1)利用三角形的外角的性质即可解决问题;
(2)过点A作AM⊥BC于M,过点D作DH⊥AB于H,构建直角三角形,利用特殊角的三角函数值求出BM、CM,设设BH=DH=x,利用三角函数列出方程,求出BD,进而求得答案;
(3)根据主从联动的原理,可知点F的轨迹是线段BC顺时针旋转45度,再缩短为根号二分之一,求出BC即可.
解:(1)如图1,
∵将线段AD绕A顺时针旋转90°,得到线段AE,
∴AE=AD,∠AED=∠ADE=45°
∵∠B=45°,
∴∠EDC=∠B+∠AED=90°
故答案为:90°
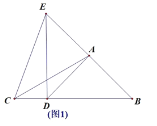
(2)如图2,过点A作AM⊥BC于M,过点D作DH⊥AB于H,
在Rt△ABM中,∠B=45°, AM⊥BC,AB=4,
∴AM=BM=![]()
在Rt△DHB中,∠B=45°, DH⊥AB,设BH=DH=x,
∴BD=![]()
在Rt△AMC中,∠AMC=90°, ∠ACB=30°,
∴![]()
∴![]()
∴CM=![]()
∵DE⊥AC,AE=AD
∴AC是线段DE的垂直平分线,
∴CD=CE,∠ECA=∠DCA=30°
∴∠ECD=60°
∴△CDE是等边三角形
∴∠EDC=60°,CD=DE
∴∠ADH=180°-∠EDC-∠ADE-∠BDH=30°
在Rt△ADH中,AH=4-x,
∴tan∠ADH=![]()
∴AH=![]()
∴![]() =4-x,
=4-x,
∴![]()
∴BD=![]()
∴DM=BD-BM=![]() =
=![]()
∴CD=CM-DM=![]() -(
-(![]() )=
)=![]()
∴DE=![]()
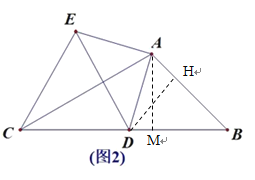
(3)如图3,连接AF,过A作AM⊥BC,
∵△ADE为等腰直角三角形,F为ED中点,
∴∠DAF=45°,![]()
∴AF相当于AD逆时针旋转了45°,再变为![]() AD,
AD,
又∵点D轨迹为BC,∴点F的轨迹为BC逆时针旋转45°,再变为![]() BC,
BC,
在等腰Rt△ABM中,AB=![]() ,∴AM=BM=
,∴AM=BM=![]()
在Rt△ACM中,∠ACM=30°,
∴tan30°=![]() ,
,
∴CM=![]()
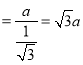
∴BC=CM+BM=![]()
∴点F的路径为:![]() BC=
BC=![]()
所以点F的路径为:![]()

 高中必刷题系列答案
高中必刷题系列答案【题目】随机抽取某城市天的空气质量状况统计如下:
污染指数( |
|
|
|
|
|
|
天数( |
|
|
|
|
|
|
(其中![]() 时,空气质量为优;
时,空气质量为优;![]() 时,空气质量为良;
时,空气质量为良;![]() 时,空气质量为轻微污染)
时,空气质量为轻微污染)
(1)这![]() 天中,空气质量为轻微污染的天数所占的百分数是多少?
天中,空气质量为轻微污染的天数所占的百分数是多少?
(2)估计该城市一年(以![]() 天记)中有多少天空气质量到良以上?
天记)中有多少天空气质量到良以上?
(3)保护环境人人有责,请说出一种保护环境的好方法.