题目内容
【题目】【探索新知】
已知平面上有n(n为大于或等于2的正整数)个点A1 , A2 , A3 , …An , 从第1个点A1开始沿直线滑动到另一个点,且同时满足以下三个条件:①每次滑动的距离都尽可能最大;②n次滑动将每个点全部到达一次;③滑动n次后必须回到第1个点A1 , 我们称此滑动为“完美运动”,且称所有点为“完美运动”的滑动点,记完成n个点的“完美运动”的路程之和为Sn .
(1)如图1,滑动点是边长为a的等边三角形三个顶点,此时S3=;
(2)如图2,滑动点是边长为a,对角线(线段A1A2、A2A4)长为b的正方形四个顶点,此时S4= .
【深入研究】
现有n个点恰好在同一直线上,相邻两点距离都为1,
(3)如图3,当n=3时,直线上的点分别为A1、A2、A3 .
为了完成“完美运动”,滑动的步骤给出如图4所示的两种方法:
方法1:A1→A3→A2→A1 , 方法2:A1→A2→A3→A1 .
①其中正确的方法为 .
A.方法1 B.方法2 C.方法1和方法2
②完成此“完美运动”的S3= . 

(4)当n分别取4,5时,对应的S4= , S5=
(5)若直线上有n个点,请用含n的代数式表示Sn .
【答案】
(1)3a
(2)2a+2b
(3)A;4
(4)8;12
(5)
解:n 为奇数时:Sn=n﹣1+n﹣2+…+1+ ![]() ﹣1=
﹣1= ![]() ;
;
n 为偶数时:Sn=n﹣1+n﹣2+…+1+ ![]() =
= ![]()
【解析】解:(1)如图1,∵滑动点是边长为a的等边三角形三个顶点,
∴S3=3a,
所以答案是:3a;(2)如图2,∵滑动点是边长为a,对角线长为b的正方形四个顶点,
∴S4=2a+2b,
所以答案是:2a+2b;(3)如图4,①∵方法2 是错的,不满足第①个条件,每一次距离要是最大的,
∴方法1正确,
故选A;②如图3,S3=2+1+1=4,
所以答案是:4;(4)根据条件:①每次滑动的距离都尽可能最大;②n次滑动将每个点全部到达一次;③滑动n次后必须回到第1个点A1 , 可得:
S4=3+2+1+2=8,
S5=4+3+2+1+2=12,
所以答案是:8,12;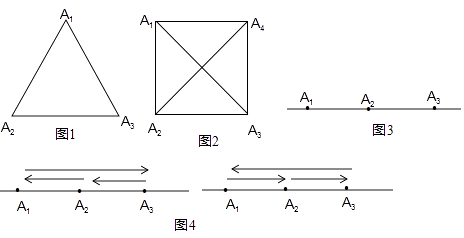

 阅读快车系列答案
阅读快车系列答案