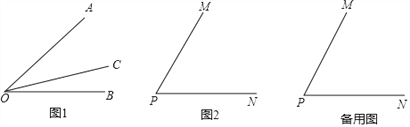
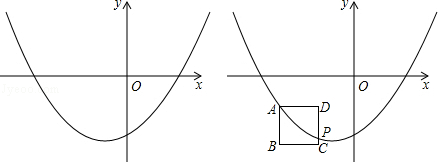
��Ŀ����
����Ŀ����ͼ����֪�����߾���ԭ��O��x������һ��A�����ĶԳ���x=2��x�ύ�ڵ�C��ֱ��y=��2x��1������������һ��B����2��m��������y�ᡢֱ��x=2�ֱ��ڵ�D��E��
��1����m��ֵ���������߶�Ӧ�ĺ�����ϵʽ��
��2���ж�ֱ��BE�������߽���ĸ�����
��3����֤��CD��ֱƽ��BE��
��4����P�Ǹ��������ϵ�һ�����㣬�Ƿ���������ĵ�P��ʹ�á�PBE�ǵ���ֱ�������Σ��ҡ�PEB=90�㣿�����ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�ߵ�B����2��m����ֱ����y=��2x��1�ϣ�
��m=��2������2����1=3��
��B����2��3����
�������߾���ԭ��O�͵�A���Գ���Ϊx=2��
���A��������4��0����
������������߶�Ӧ������ϵʽΪy=ax��x��4����
����B����2��3��������ʽ��
3=��2a������2��4������ã�a= ![]() ��
��
������������߶�Ӧ�ĺ�����ϵʽΪy= ![]() x��x��4��=
x��x��4��= ![]() x2��x
x2��x
��2��
�⣺��y=��2x��1����y= ![]() x2��x���ã�
x2��x���ã� ![]() x2��x=��2x��1��
x2��x=��2x��1��
�����ã�x2+4x+4=0��
���=42��4��1��4=0��
��ֱ��BE��������ֻ��һ������
��3��
�⣺֤������x=2ʱ��y=��2x��1=��5��
��E��2����5����
��C��2��0����B����2��3����
��CE=0������5��=5��CB= ![]() =5��
=5��
��CE=CB��
��D��0����1����B����2��3����E��2����5����
��BD= ![]() =2
=2 ![]() ��DE=
��DE= ![]() =2
=2 ![]() ��
��
��BD=DE��
��CD��ֱƽ��BE
��4��
�⣺�����ڣ��������£�
����E��ME��BE��x���ڵ�M������B��BN��ֱ��x=2�ڵ�N����ͼ��ʾ��
��B����2��3����E��2����5����
��BN=2������2��=4��EN=3������5��=8��CE=0������5��=5��
�ߡ�BEN+��EBN=90�㣬��BEN+��MEC=90�㣬
���EBN=��MEC��
���EBN�ס�MEC��
�� ![]() ��
��
��MC=10��
��M��12��0����
��ֱ��EM�ĺ�����ϵʽΪy=kx+b��k��0����
��E��2����5����M��12��0������y=kx+b��
![]() ����ã�
����ã� 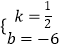 ��
��
��ֱ��EM�ĺ�����ϵʽΪy= ![]() x��6��
x��6��
��y= ![]() x��6����y=
x��6����y= ![]() x2��x���ã�
x2��x���ã� ![]() x2��x=
x2��x= ![]() x��6��
x��6��
�����ã�x2��6x+24=0��
���=����6��2��4��1��24=��60��0��
��ֱ��EM�����������㣬
��������������ĵ�P��
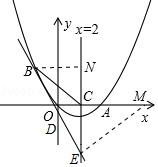
����������1�����ݵ�B�ĺ���������һ�κ���ͼ���ϵ�������������������B�����꣬���ݵ�O�������������ߵĶԳ��ἴ���ҳ���A�����꣬�������ߵĺ�����ϵʽΪy=ax��x��4���������B���������aֵ���ɣ���2����ֱ��BE�ĺ�����ϵʽ���������ߵĺ�����ϵʽ�пɵó�����x��һԪ���η��̣��ɸ����б�ʽ��=0�����ɵó�ֱ��BE��������ֻ��һ�����㣻��3�����ݵ�E�ĺ���������һ�κ���ͼ���ϵ�������������������E�����꣬��ϵ�B��C���������������ľ��빫ʽ�����ɵó�CE=CB���ٸ��ݵ�B��D��E���������������ľ��빫ʽ�����ɵó�BD=DE�����ݵ��������ε����ߺ�һ����֤��CD��ֱƽ��BE����4������E��ME��BE��x���ڵ�M������B��BN��ֱ��x=2�ڵ�N�����EBN�ס�MEC���������������ε����ʼ����ҳ���M�����꣬�ɵ�E��M���������ô���ϵ���������ֱ��EM�ĺ�����ϵʽ��������������ߵĺ�����ϵʽ�пɵó�����x��һԪ���η��̣��ɸ����б�ʽ��=��60��0�����ɵó�ֱ��EM�����������㣬�ɴ˵ó����������������ĵ�P��
�����㾫����������Ҫ�����˶��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ�㣬��Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮

 ��������ϵ�д�
��������ϵ�д�����Ŀ���������õ������ϰ�ߣ���ѧ����ѧϰ������dz�����![]() ij��ѧΪ���˽����꼶ѧ��������������У���̴������꼶�����ȡ�˲���ѧ����������Щѧ��ͨ�������һ��������ʱ��
ij��ѧΪ���˽����꼶ѧ��������������У���̴������꼶�����ȡ�˲���ѧ����������Щѧ��ͨ�������һ��������ʱ��![]() ����
����![]() �����˵���
�����˵���![]() �ְѵ�������ΪA��B��C��D���飬���±���ʾ��ͬʱ�������������Ƴ�����������������ͳ��ͼ��
�ְѵ�������ΪA��B��C��D���飬���±���ʾ��ͬʱ�������������Ƴ�����������������ͳ��ͼ��

��� | �����ʱ�� |
A |
|
B |
|
C |
|
D |
|
����������ṩ����Ϣ������������⣺
![]() ����ͳ��ͼ��D�������ε�Բ�ĽǶ���Ϊ______��
����ͳ��ͼ��D�������ε�Բ�ĽǶ���Ϊ______��
![]() ��ȫƵ���ֲ�ֱ��ͼ��
��ȫƵ���ֲ�ֱ��ͼ��
![]() ��֪��У���꼶����1200��ѧ���������������꼶ѧ�����ж�����һ���������ʱ�䲻����20���ӣ�
��֪��У���꼶����1200��ѧ���������������꼶ѧ�����ж�����һ���������ʱ�䲻����20���ӣ�