Question

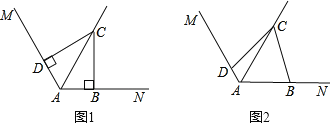
【题目】已知∠MAN=120°，AC平分∠MAN，点B、D分别在AN、AM上．

（1）如图1，若∠ABC=∠ADC=90°，请你探索线段AD、AB、AC之间的数量关系，并证明之；

（2）如图2，若∠ABC+∠ADC=180°，则（1）中的结论是否仍然成立？若成立，给出证明；若不成立，请说明理由．

Answer 1

【答案】（1）AD+AB=AC；（2）仍成立．

【解析】

（1）得到∠ACD＝∠ACB＝30°后再可以证得AD＝ABAC从而，证得结论；

（2）过点C分别作AM、AN的垂线，垂足分别为E、F，证得△CED≌△CFB后即可得到AD+AB＝AE﹣ED+AF+FB＝AE+AF，从而证得结论．

（1）关系是：AD+AB＝AC．证明如下：

∵AC平分∠MAN，∠MAN＝120°，∴∠CAD＝∠CAB＝60°．

又∵∠ADC＝∠ABC＝90°，∴∠ACD＝∠ACB＝30°，则AD＝ABAC（直角三角形一锐角为30°，则它所对直角边为斜边一半），∴AD+AB＝AC．

（2）仍成立．理由如下：

过点C分别作AM、AN的垂线，垂足分别为E、F．

∵AC平分∠MAN，∴CE＝CF（角平分线上点到角两边距离相等）．

∵∠ABC+∠ADC＝180°，∠ADC+∠CDE＝180°，∴∠CDE＝∠ABC．

又∵∠CED＝∠CFB＝90°，∴△CED≌△CFB（AAS）．

∵ED＝FB，∴AD+AB＝AE﹣ED+AF+FB＝AE+AF．

由（1）知AE+AF＝AC，∴AD+AB＝AC．