题目内容
【题目】矩形ABCO中，O（0，0），C（0，3），A（a，0），（a≥3），以A为旋转中心顺时针旋转矩形ABCO得到矩形AFED．
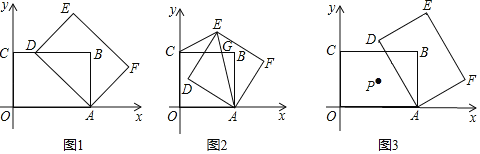
（1）如图1，当点D落在边BC上时，求BD的长（用a的式子表示）；
（2）如图2，当a＝3时，矩形AFED的对角线AE交矩形ABCO的边BC于点G，连结CE，若△CGE是等腰三角形，求直线BE的解析式；
（3）如图3，矩形ABCO的对称中心为点P，当P，B关于AD对称时，求出a的值，此时在x轴、y轴上是否分别存在M，N使得四边形EFMN为平行四边形，若存在直接写出M，N坐标，不存在说明理由．
【答案】（1）BD＝
；（2）y＝﹣x+6；（3）M（
，0），N（0，
）
【解析】
（1）如图1，当点D落在边BC上时，BD2=AD2-AB2，即可求解；
（2）分CG=EG、CE=GE、CE=CG三种情况分别求解；
（3）①由点P为矩形ABCO的对称中心，得到
求得直线PB的解析式为
，得到直线AD的解析式为：
，解方程即可得到结论；②根据①中的结论得到直线AD 的解析式为
，求得∠DAB=30°，连接AE，推出A，B，E三点共线，求得
，设M（m，0），N（0，n），解方程组即可得到结论．
（1）如图1，
在矩形ABCO中，∠B＝90°
当点D落在边BC上时，BD2＝AD2﹣AB2，
∵C（0，3），A（a，0）
∴AB＝OC＝3，AD＝AO＝a，
∴BD＝；
（2）如图2，连结AC，
∵a＝3，∴OA＝OC＝3，
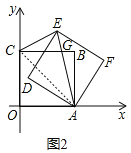
∴矩形ABCO是正方形，∴∠BCA＝45°，
设∠ECG的度数为x，
∴AE＝AC，∴∠AEC＝∠ACE＝45°+x，
①当CG＝EG时，x＝45°+x，
解得x＝0，不合题意，舍去；
②当CE＝GE时，如图2，
∠ECG＝∠EGC＝x
∵∠ECG+∠EGC+∠CEG＝180°，
∴x+x+（45°+x）＝180°，解得x＝45°，
∴∠AEC＝∠ACE＝90°，不合题意，舍去；
③当CE＝CG时，∠CEG＝∠CGE＝45°+x，
∵∠ECG+∠EGC+∠CEG＝180°，
∴x+（45°+x）+（45°+x）＝180°，解得x＝30°，
∴∠AEC＝∠ACE＝75°，∠CAE＝30°
如图3，连结OB，交AC于点Q，过E作EH⊥AC于H，连结BE，
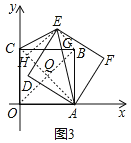
∴EH＝
AE＝AC，BQ＝AC，
∴EH＝BQ，EH∥BQ且∠EHQ＝90°
∴四边形EHQB是矩形
∴BE∥AC，
设直线BE的解析式为y＝﹣x+b，
∵点B（3，3）在直线上，则b＝6，
∴直线BE的解析式为y＝﹣x+6；
（3）①∵点P为矩形ABCO的对称中心，
∴，
∵B（a，3），
∴PB的中点坐标为：
，
∴直线PB的解析式为，
∵当P，B关于AD对称，
∴AD⊥PB，
∴直线AD的解析式为：，
∵直线AD过点
，∴
，
解得：a＝±3
，
∵a≥3，
∴a＝3；
②存在M，N；
理由：∵a＝3，
∴直线AD 的解析式为y＝﹣x+9，
∴∴∠DAO＝60°，
∴∠DAB＝30°，
连接AE，
∵AD＝OA＝3，DE＝OC＝3，
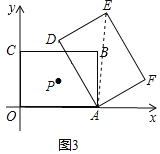
∴∠EAD＝30°，
∴A，B，E三点共线，
∴AE＝2DE＝6，
∴，
设M（m，0），N（0，n），
∵四边形EFMN是平行四边形，
∴
，
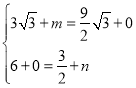解得：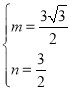
，
∴M（，0），N（0，）．
