Question

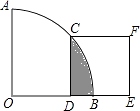
【题目】矩形纸片ABCD中，AB=3cm，BC=4cm，现将纸片折叠压平，使A与C重合，设折痕为EF，则重叠部分△AEF的面积等于 ．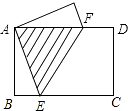

Answer 1

【答案】
【解析】解：设AE=x，由折叠可知，EC=x，BE=4﹣x， 在Rt△ABE中，AB2+BE2=AE2 ， 即32+（4﹣x）2=x2 ，
解得：x=
由折叠可知∠AEF=∠CEF，
∵AD∥BC，
∴∠CEF=∠AFE，
∴∠AEF=∠AFE，即AE=AF= ，
∴S△AEF= ×AF×AB= × ×3= ．
故答案为： ．
要求重叠部分△AEF的面积，选择AF作为底，高就等于AB的长；而由折叠可知∠AEF=∠CEF，由平行得∠CEF=∠AFE，代换后，可知AE=AF，问题转化为在Rt△ABE中求
AE．