题目内容
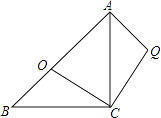
【题目】如图，在△ABC中，AC=BC，AD平分∠BAC，∠ADC=60°，求∠C的度数．
【答案】100°
【解析】试题设∠BAD=x．由AD平分∠BAC，得出∠CAD=∠BAD=x，∠BAC=2∠BAD=2x．由AC=BC，得出∠B=∠BAC=2x．根据三角形外角的性质得出∠ADC=∠B+∠BAD=60°，即2x+x=60°，求得x=20°，那么∠B=∠BAC=40°．然后在△ABC中，根据三角形内角和定理得出∠C=180°-∠B-∠BAC=100°．
试题解析：设∠BAD=x．
∵AD平分∠BAC，
∴∠CAD=∠BAD=x，∠BAC=2∠BAD=2x．
∵AC=BC，
∴∠B=∠BAC=2x．
∵∠ADC=∠B+∠BAD=60°，
∴2x+x=60°，
∴x=20°，
∴∠B=∠BAC=40°．
在△ABC中，∵∠BAC+∠B+∠C=180°，
∴∠C=180°-∠B-∠BAC=100°．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
相关题目
