Question

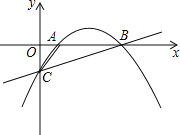
【题目】成都市某企业积极响应政府“创新发展”的号召，研发了一种新产品．已知研发、生产这种新产品的成本为30元/件，经市场调查发现，该产品的年销售量y（万件）与销售单价x（元）之间的函数关系如下图：

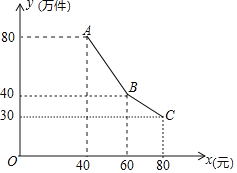
（1）求出y与x之间的函数关系式；

（2）当该产品的售价为多少时，该企业销售该产品获得的年利润最大？最大年利润是多少？（注：年利润＝年销售量×（销售单价﹣成本单价））

Answer 1

【答案】（1）y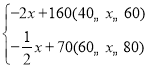＝；（2）当该产品的售价为80元/件时，该企业销售该产品获得的年利润最大；最大年利润是1500万元．

【解析】

（1）当40≤x≤60时，当60≤x≤80时，分别利用待定系数法求函数解析式；

（2）设年利润为为w万元．当40≤x≤60时，当60≤x≤80时，列函数关系式．根据二次函数的性质即可得到结论．

解：（1）当40≤x≤60时，

设线段AB所在直线解析式为y＝k1x+b1，

将A（40，80），B（60，40）代入有，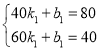

解之得，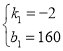

∴y＝﹣2x+160（40≤x≤60），

同理当60≤x≤80时，设线段BC所在直线解析式为y＝k2x+b2

将B，C坐标代入可得

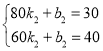
解得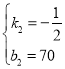

∴ （60≤x≤80）

∴y与x之间的函数关系式为：y＝；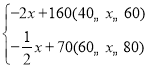

（2）设年利润为为w万元．

当40≤x≤60时，w＝（x﹣30）（﹣2x+160）＝﹣（x﹣55）2+1250，

当x＝55时，w最大＝1250；

当60≤x≤80时，w＝（x﹣30）（﹣x+70）＝﹣（x﹣85）2+，

又60≤x≤80，∴当x＝80时，w最大＝1500，

∵1250＜1500，

∴当该产品的售价为80元/件时，该企业销售该产品获得的年利润最大；最大年利润是1500万元．