Question

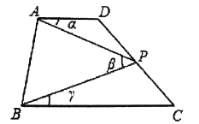
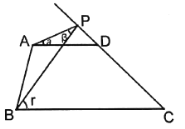
【题目】如图,若果∠1＝∠2，那么添加下列任何一个条件：（1），（2），（3）∠B＝∠D，（4）∠C＝∠AED， 其中能判定△ABC∽△ADE的个数为

A. 1 B. 2 C. 3 D. 4

Answer 1

【答案】C

【解析】∵∠1＝∠2，

∴∠1+∠BAE=∠2+∠BAE，即∠DAE=∠BAC，

∴（1）当添加条件“”时，可由“两边对应成比例，且夹角相等的两个三角形相似”证得：△ABC∽△ADE；

（2）当添加条件“”时，不能证明：△ABC∽△ADE；

（3）当添加条件“∠B＝∠D”时，可由“有两个角对应相等的两个三角形相似”证得：△ABC∽△ADE；

（4）当添加条件“∠C＝∠AED”时，可由“有两个角对应相等的两个三角形相似”证得：△ABC∽△ADE；

综上所述，添加上述条件中的1个后，能证明△ABC∽△ADE的共有3个.

故选C.