题目内容
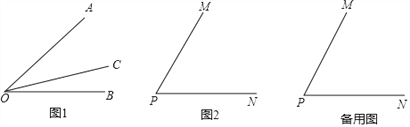
【题目】如图,![]() 中,
中,![]() ,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为每秒1个单位长度,点N的运度为每秒2个单位长度
,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为每秒1个单位长度,点N的运度为每秒2个单位长度![]() 当点M第一次到达B点时,M、N同时停止运动.
当点M第一次到达B点时,M、N同时停止运动.![]() 点M、N运动几秒后,M、N两点重合?
点M、N运动几秒后,M、N两点重合?![]() 点M、N运动几秒后,可得到等边三角形
点M、N运动几秒后,可得到等边三角形![]() ?
?![]() 当点M、N在BC边上运动时,能否得到以MN为底边的等腰
当点M、N在BC边上运动时,能否得到以MN为底边的等腰![]() ?如存在,请求出此时M、N运动的时间.
?如存在,请求出此时M、N运动的时间.
【答案】(1)点M、N运动12秒后,M、N两点重合;(2)点M、N运动4秒后,可得到等边三角形![]() ;(3)当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形,此时M、N运动的时间为16秒.
;(3)当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形,此时M、N运动的时间为16秒.
【解析】
(1)根据路程差=12构建方程即可解决问题;
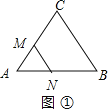
(2)设点M、N运动t秒后,可得到等边三角形△AMN,如图①中,根据AM=AN,构建方程即可解决问题;
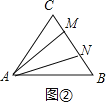
(3)当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,由(1)知12秒时M、N两点重合,恰好在C处,如图②,假设△AMN是等腰三角形,根据CN=BN,构建方程即可解决问题.
![]() 设点M、N运动x秒后,M、N两点重合,
设点M、N运动x秒后,M、N两点重合,
![]() ,
,
解得:![]() ;
;
![]() 点M、N运动12秒后,M、N两点重合.
点M、N运动12秒后,M、N两点重合.
![]() 设点M、N运动t秒后,可得到等边三角形
设点M、N运动t秒后,可得到等边三角形![]() ,如图
,如图![]()
![]() ,
,![]() ,
,
![]() 三角形
三角形![]() 是等边三角形,
是等边三角形,
![]() ,
,
解得![]() ,
,
![]() 点M、N运动4秒后,可得到等边三角形
点M、N运动4秒后,可得到等边三角形![]() .
.
![]() 当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由![]() 知12秒时M、N两点重合,恰好在C处,
知12秒时M、N两点重合,恰好在C处,
如图![]() ,假设
,假设![]() 是等腰三角形,
是等腰三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
在![]() 和
和![]() 中,
中,
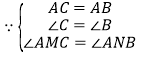 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,![]() 是等腰三角形,
是等腰三角形,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
解得:![]() 故假设成立.
故假设成立.
![]() 当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形,此时M、N运动的时间为16秒.
当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形,此时M、N运动的时间为16秒.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部水果都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
【题目】养成良好的早锻炼习惯,对学生的学习和生活非常有益![]() 某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间
某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间![]() 分钟
分钟![]() 进行了调查
进行了调查![]() 现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.

组别 | 早锻炼时间 |
A |
|
B |
|
C |
|
D |
|
请根据以上提供的信息,解答下列问题:
![]() 扇形统计图中D所在扇形的圆心角度数为______;
扇形统计图中D所在扇形的圆心角度数为______;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.
已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.