Question

【题目】在平面直角坐标系中，抛物线与轴的交点为，

(1)求抛物线的顶点坐标；

(2)若，

①求抛物线的解析式；

②)已知点,，将抛物线在的部分向上平移个单位得到图象，若图象与线段恰有个公共点，结合函数的图象，直接写出的取值范围.

Answer 1

【答案】（1）；（2）①；② 或.

．

【解析】

（1）函数对称轴为：x=，再把x=1代入解析式，即可求解；
（2）①由，对称轴为直线，求出A,B两点 ，即可求解；

②根据题意画出图形，结合函数图象即可解答.

(1)根据题意可知：

代入，得.

则顶点为

(2)①由，对称轴为直线，

得，

故，

∴解析式为

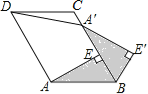
②如图所示，

点A到EF=4-3=1，

点B到EF=4+（）

点C到EF=4+1=5，

∴结合函数图象可知的取值范围为 或.

故答案为： 或.