题目内容
如图,平面直角坐标系中,抛物线y=-x2+3x+4与x轴交于点A、B(A在左侧),与y轴交于点C,抛物线的顶点为点M,对称轴与线段BC交于点N,点P为线段BC上一个动点(与B、C不重合) .
1.求点A、B的坐标;
2.在抛物线的对称轴上找一点D,使|DC-DB|的值最大,求点D的坐标;
3.过点P作PQ∥y轴与抛物线交于点Q,连接QM,当四边形PQMN满足有一组对边相等时,求P点坐标.

1.A(-1,0)、B(4,0)
2.连结AC并延长交抛物线的对称轴于D
求出直线AC解析式:![]()
求出D点坐标(1.5,10)

3.N坐标是(1.5,2.5)M坐标是(![]() )
)
设P(![]() ),Q(
),Q(![]() )
)
①四边形PQMN是平行四边形,此时PQ=MN
由题意得,![]() =(
=(![]() )-(-
)-(-![]() )
)
解得![]() =2.5,
=2.5,![]() =1.5(舍去)此时P(2.5,1.5),
=1.5(舍去)此时P(2.5,1.5),
②四边形PQMN是等腰梯形,此时PN=QM
进一步得MG=NH(QG、 PH是所添的垂线段)
从而得方程![]()
解得![]() =0.5,
=0.5,![]() =1.5(舍去)
=1.5(舍去)
此时P(0.5,3.5),
综合上述两种情况可知:当四边形PQMN满足有一组对边相等时,P点的坐标为(2.5,1.5)或(0.5,3.5)
解析:此题注意满足四边形有一组对边相等有两种情况:平行四边形和等腰梯形。

练习册系列答案
相关题目
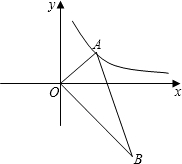 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线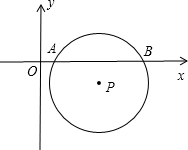 =2
=2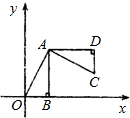 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
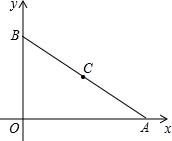 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.