题目内容
 如图,已知Rt△ABC的锐角顶点A在反比例函数y=
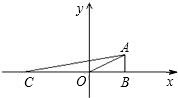
如图,已知Rt△ABC的锐角顶点A在反比例函数y= 的图象上,且△AOB的面积为3,OB=3,求:
的图象上,且△AOB的面积为3,OB=3,求:
(1)点A的坐标;
(2)函数y= 的解析式;
的解析式;
(3)直线AC的函数关系式为y= x+
x+ ,求△ABC的面积.
,求△ABC的面积.
解:(1)∵SRt△AOB= •OB•AB,
•OB•AB,
∴3= ×3•AB.
×3•AB.
得AB=2.
∴A(3,2).
(2)∵点A在反比例函数y= 的图象上,
的图象上,
∴2= ,m=6.
,m=6.
∴反比例函数解析式为y= ;
;
(3)当y=0时,0= x+
x+ ,
,
解得x=-4.
∴OC=4,BC=4+3=7.
∴S△ABC= BC•AB=
BC•AB= ×7×2=7.
×7×2=7.
分析:(1)根据题意,只需求AB的长即可得到A的坐标.由三角形AOB的面积易求解;
(2)因为A点在反比例函数的图象上,所以根据A的坐标即可求出函数解析式;
(3)根据直线解析式求C的坐标,得OC的长,从而得BC的长.根据面积公式求解.
点评:此题考查了用待定系数法求反比例函数的解析式及相关图形面积的计算,属基础题.
 •OB•AB,
•OB•AB,∴3=
 ×3•AB.
×3•AB.得AB=2.
∴A(3,2).
(2)∵点A在反比例函数y=
 的图象上,
的图象上,∴2=
 ,m=6.
,m=6.∴反比例函数解析式为y=
 ;
;(3)当y=0时,0=
 x+
x+ ,
,解得x=-4.
∴OC=4,BC=4+3=7.
∴S△ABC=
 BC•AB=
BC•AB= ×7×2=7.
×7×2=7.分析:(1)根据题意,只需求AB的长即可得到A的坐标.由三角形AOB的面积易求解;
(2)因为A点在反比例函数的图象上,所以根据A的坐标即可求出函数解析式;
(3)根据直线解析式求C的坐标,得OC的长,从而得BC的长.根据面积公式求解.
点评:此题考查了用待定系数法求反比例函数的解析式及相关图形面积的计算,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.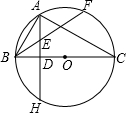 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF. 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P. 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为