题目内容
如图,△ABC内接于⊙O,弦AC交直径BD于点E,AG⊥BD于点G,延长AG交BC于点F. 求证:AB2=BF·BC.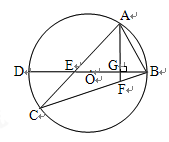

证明:延长AF,交⊙O于H.
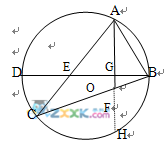
∵直径BD⊥AH,∴= . ……………………2分
∴∠C=∠BAF. ………………………3分
在△ABF和△CBA中,
∵∠BAF =∠C,∠ABF=∠CBA,
∴△ABF∽△CBA. …………………………………………4分
 ∴
∴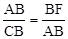 ,即AB2=BF×BC.
,即AB2=BF×BC.  …………………………………………5分
…………………………………………5分
证明2:连结AD,
∵BD是直径,∴∠BAG+∠DAG=90°. ……………………1分
∵AG⊥BD,∴∠DAG+∠D=90°.
∴∠BAF =∠BAG =∠D. ……………………2分
又∵∠C =∠D,
∴∠BAF=∠C. ………………………3分

∵直径BD⊥AH,∴= . ……………………2分
∴∠C=∠BAF. ………………………3分
在△ABF和△CBA中,
∵∠BAF =∠C,∠ABF=∠CBA,
∴△ABF∽△CBA. …………………………………………4分
 ∴
∴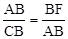 ,即AB2=BF×BC.
,即AB2=BF×BC.  …………………………………………5分
…………………………………………5分证明2:连结AD,
∵BD是直径,∴∠BAG+∠DAG=90°. ……………………1分
∵AG⊥BD,∴∠DAG+∠D=90°.
∴∠BAF =∠BAG =∠D. ……………………2分
又∵∠C =∠D,
∴∠BAF=∠C. ………………………3分
略

练习册系列答案
相关题目

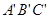 是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
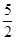 ,3),则A′的坐标为 ;
,3),则A′的坐标为 ;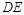 是
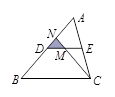
是 的中位线,
的中位线, 是
是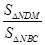 = .
= .
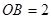 ,
,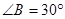 ,点C是弦AB上一动点(不与点A、B重合),连结CO并延长交⊙O于点D,连结AD.
,点C是弦AB上一动点(不与点A、B重合),连结CO并延长交⊙O于点D,连结AD.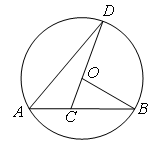
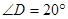 时,求
时,求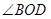 的度数;
的度数;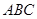 中,
中,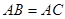 ,以
,以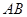 为直径的⊙O分别交
为直径的⊙O分别交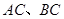 于点
于点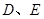 , 点
, 点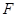 在
在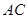 的延长线上,且
的延长线上,且 ∠
∠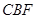
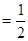 ∠
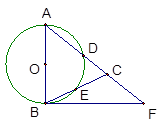
∠ 。
。
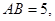 sin∠CBF=
sin∠CBF=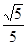 , 求BC和BF的长。
, 求BC和BF的长。 中,DE//BC,且AE=3cm,EC=5cm,DE=6cm,则BC等于( )
中,DE//BC,且AE=3cm,EC=5cm,DE=6cm,则BC等于( )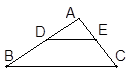
 AB=12.动点P、Q分别在边AD和BC上,且BQ=3DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x
AB=12.动点P、Q分别在边AD和BC上,且BQ=3DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x
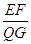 的值.
的值.