题目内容
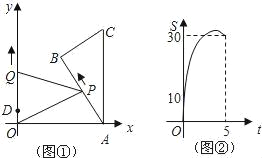
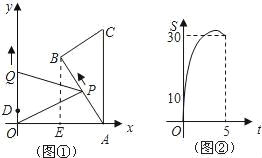
【题目】如图①,Rt△ABC中,∠B=90°∠CAB=30°,AC⊥x轴.它的顶点A的坐标为(10,0),顶点B的坐标为(5,5![]() ),点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
),点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
(1)求∠BAO的度数.(直接写出结果)
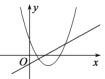
(2)当点P在AB上运动时,△OPQ的面积S与时间t(秒)之间的函数图象为抛物线的一部分(如图②),求点P的运动速度.
(3)求题(2)中面积S与时间t之间的函数关系式,及面积S取最大值时,点P的坐标.
(4)如果点P,Q保持题(2)中的速度不变,当t取何值时,PO=PQ,请说明理由.
【答案】(1)∠BAO=60°; (2)点P的运动速度为2个单位/秒;(3)P(![]() ,
,![]() );(4)t=
);(4)t=![]() 时,PO=PQ.
时,PO=PQ.
【解析】
(1)利用∠BAO的正切值,求出∠BAO的度数即可;
(2)利用图②中的函数图象,求得点P的运动时间与路程解决即可;
(3)利用特殊角的三角函数,三角形的面积以及配方法解决问题;
(4)分两种情况进行列方程解决问题.
(1)如图,
过点B作BE⊥OA于E,则OE=5,BE=5,OA=10,
∴AE=5,Rt△ABE中,tan∠BAO=![]() ,
,
∴∠BAO=60°;
(2)由图形可知,当点P运动了5秒时,它到达点B,此时AB=10,因此点P的运动速度为10÷5=2个单位/秒,
点P的运动速度为2个单位/秒;
(3)P(10﹣t,![]() t)(0≤t≤5),
t)(0≤t≤5),
∵S=![]() (2t+2)(10﹣t),
(2t+2)(10﹣t),
=﹣(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,S有最大值为
时,S有最大值为![]() ,
,
此时P(![]() );
);
(4)当P在AB上时,根据P点纵坐标得出:
![]() ,
,
解得:t=![]() ,
,
当P在BC上时,![]() ,
,
此方程无解,故t不存在,
综上所知当t=![]() 时,PO=PQ.
时,PO=PQ.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案