题目内容
【题目】在Rt△ACB中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
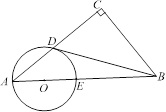
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD∶AO=8∶5,BC=3,求BD的长.
【答案】(1)见解析;(2)BD=![]() .
.
【解析】试题分析:(1)由等腰三角形的性质和已知得出∠ODA=∠CBD,由直角三角形的性质得出∠CBD+∠CDB=90°,因此∠ODA+∠CDB=90°,得出∠ODB=90°,即可得出结论;(2)设AD=8k,则AO=5k,AE=2OA=10k,由圆周角定理得出∠ADE=90°,△ADE∽△BCD,得出对应边成比例![]() ,即可求出BD的长.
,即可求出BD的长.
试题解析:(1)BD是⊙O的切线;理由如下:∵OA=OD,∴∠ODA=∠A,∵∠CBD=∠A,∴∠ODA=∠CBD,∵∠C=90°,∴∠CBD+∠CDB=90°,∴∠ODA+∠CDB=90°,∴∠ODB=90°,即BD⊥OD,∴BD是⊙O的切线;(2)设AD=8k,则AO=5k,AE=2OA=10k,∵AE是⊙O的直径,∴∠ADE=90°,∴∠ADE=∠C,又∵∠CBD=∠A,∴△ADE∽△BCD,∴![]() ,即
,即![]() ,解得:BD=
,解得:BD=![]() .所以BD的长是
.所以BD的长是![]() .
.

练习册系列答案
相关题目