题目内容
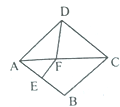
【题目】如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，点F是CD的中点，且AF⊥AB，若AD=2.7，AF=4，AB=6，则CE的长为（ ）
A. 2
B. 2
-1 C. 2.5 D. 2.3
【答案】D
【解析】分析：延长AF至BC延长线上交于G点，由已知可证明∠AGB=∠EAG，则EF为△ABG的中位线，得出EF=3，还可证明FG=4，由勾股定理得EG=5，则求得CE的长为2.3．
详解：延长AF、BC交于点G．
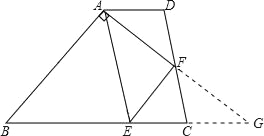
∵AD∥BC，
∴∠D=∠FCG，∠DAF=∠G．
又DF=CF，
∴△AFD≌△GFC．
∴AG=2AF=8，CG=AD=2.7．
∵AF⊥AB，AB=6，
∴BG=10．
∴BC=BG﹣CG=7.3．
∵AE=BE，
∴∠BAE=∠B．
∴∠EAG=∠AGE．
∴AE=GE．
∴BE=
BG=5．
∴CE=BC﹣BE=2.3．
故选：D．
练习册系列答案
相关题目
