题目内容
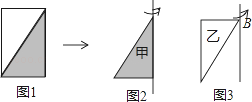
【题目】如图，甲、乙两人到距离A地35千米的B地办事，甲步行先走，乙骑车后走，两人行进的路程和时间的关系如图所示，根据图示提供的信息解答：
（1）乙比甲晚 小时出发；乙出发 小时后追上甲；
（2）求乙比甲早几小时到达B地？
【答案】（1）2； 2； （2）乙比甲早1.5小时到达B地
【解析】分析：（1）结合图象，即可得出答案；
（2）分别求出、甲乙的函数解析式，再令S＝35即可求出甲、乙分别到达B地的时间，作差即可得出答案.
详解：（1）由图象可知，乙比甲晚2小时出发；乙出发2小时后追上甲；
故答案为：2； 2；
（2）甲的路程与时间的函数解析式为 S=5t，
当S=35时，t=7，
设乙的路程与时间的函数解析式为 S=kt+b，
根据题意，得
，
解得
，
∴乙的路程与时间的函数解析式为S=10t-20，
当S=35时，t=5.5，
∴7-5.5=1.5，
答：乙比甲早1.5小时到达B地．
轻松课堂单元期中期末专题冲刺100分系列答案
【题目】今年十一黄金周期间，九寨沟7天中每天旅游人数的变化情况如下表（正数表示比9月30日多的人数，负数表示比9月30日少的人数）：
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化/万人 | +0.5 | +0.7 | +0.8 |
|
| +0.2 |
|
(1)、请判断7天内游客人数量最多和最少的各是哪一天？它们相差多少万人？（5分）
(2)、如果9月30日旅游人数为2.5万人，平均每人消费500元，请问风景区在此7天内总收入为多少万元？
【题目】为节约用水、保护水资源，本市制定了一套节约用水的管理措施，其中规定每月用水量超过m（吨）时，超过部分每吨加收环境保护费 
元．下图反映了每月收取的水费y（元）与每月用水量x（吨）之间的函数关系的图象．按上述方案，一家酒店四、五两月用水量及缴费情况如表：
月份 | 用水量x（吨） | 水费y（元） |
四月 | 35 | 59.5 |
五月 | 80 | 151 |
（1）求出m的值；
（2）写出y与x之间的函数关系式，并指出自变量x的取值范围．
