题目内容
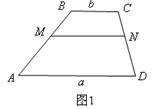
如图①,将四边形纸片ABCD沿两组对边中点连线剪切为四部分,将这四部分密铺可得到如图②所示的平行四边形,若要密铺后的平行四边形为矩形,则四边形ABCD需要满足的条件是 .


AC=BD
试题分析:密铺后的平行四边形成为矩形,必须四个内角均为直角。
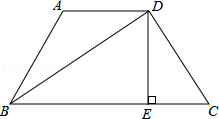
如图,连接EF、FG、GH、HE,设EG与HF交于点O,则EG⊥HF.
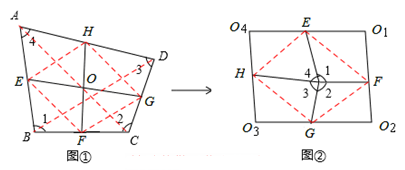
连接AC、BD,由中位线定理得:EF∥AC∥GH,且EF=GH=
 AC。
AC。∴中点四边形EFGH为平行四边形。
∴OE=OG,OH=OF。
又∵EG⊥HF,
∴由勾股定理得:EF=FG=GH=HE,即中点四边形EFGH为菱形。
∵EF=FG,EF=
 AC,FG=
AC,FG= BD,
BD,∴AC=BD。
∴四边形ABCD需要满足的条件为:AC=BD。

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目

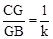 ,则
,则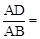 (用含k的代数式表示).
(用含k的代数式表示).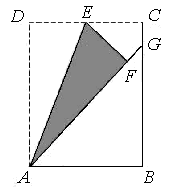
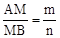 ,则有结论:
,则有结论: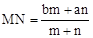 。
。