题目内容
如图：在△ABC中，AD=AE，BD=EC，∠ADB=∠AEC=105°，∠B=40°，则∠CAE= ；
35°
试题分析：根据AD=AE，BD=EC，∠ADB=∠AEC=105°，即可证得△ADB≌△AEC，从而得到AB=AC，根据等腰三角形的性质即可得到结果．
∵AD=AE，BD=EC，∠ADB=∠AEC=105°，
∴△ADB≌△AEC，
∴AB=AC，
∴∠B=∠C=40°，
在△AEC中，∠CAE+∠C+∠AEC=180°，
∴∠CAE=180°-40°-105°=35°.
点评：解答本题的关键是先证得AB=AC，再根据等腰三角形等边对等角的关系求解.
练习册系列答案
巧学巧练系列答案
相关题目
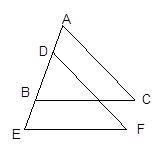
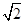m，梯子的倾斜角为45°，则这间房子的宽AB="_____________m" .