��Ŀ����
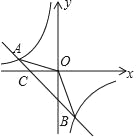
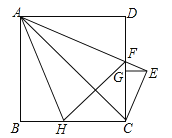
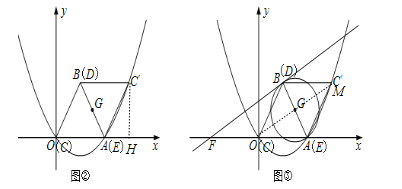
����Ŀ����ͼ�����ڣ���ƽ��ֱ������ϵ�У�һ�߳�Ϊ2�ĵȱ����ǰ�CDEǡ��������ϵ�е���OAB�غϣ��ֽ����ǰ�CDE�Ʊ�AB���е�G��G��Ҳ��DE���е㣩����˳ʱ�뷽����ת180������C��ED��λ�ã�
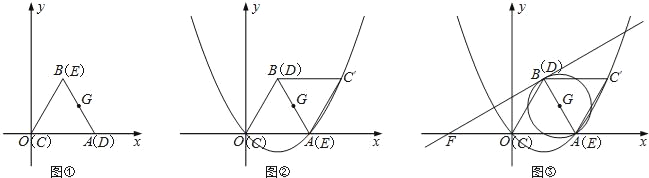
��1����C��������ꣻ
��2����O��A��C������������ߵĽ���ʽ��
��3����ͼ������G����ABΪֱ����Բ����B������G��������x���ཻ�ڵ�F��������BF�Ľ���ʽ��
��4���ڣ�3���������£����������Ƿ����һ��M��ʹ����BOF����AOM���ƣ������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1) C�䣨3��![]() ��(2) y=
��(2) y=![]() x2��
x2��![]() x (3) y=
x (3) y=![]() x+
x+![]() ��4������
��4������
����������������1����C��H��x������ͼ�������õȱ������κ���ת�����ʵõ�AC��=OA=2����OAB=��BAC��=60�㣬���C��AH=60�㣬Ȼ����ݺ�30�ȵ�ֱ�����������ߵĹ�ϵ�����AH=1��C��H=![]() ���Ӷ��õ�C�����������
���Ӷ��õ�C�����������
��2���������߽���ʽΪy=ax��x��2����Ȼ���C��������������a����
��3���������ߵ����ʵ�AB��BF�������á�FAB=60���õ�FA=2AB=4������F����2��0�������ж��ı���AOBC��Ϊ���������д��B��1��![]() ����Ȼ�����ô���ϵ������ֱ��BF�Ľ���ʽ��
����Ȼ�����ô���ϵ������ֱ��BF�Ľ���ʽ��
��4���������ߵĶԳ���Ϊֱ��x=1�������ߵĶ�������Ϊ��1����![]() �������жϡ�OBFΪ����Ϊ120���ĵ�������������������AM=AO=2ʱ����M���C���غ�����BOF���AOM�������ô�ʱM�����������OM=OAʱ����M���C������ֱ��x=1�Գ�����BOF���AOM�������ô�ʱM����������MA=MOʱ����MΪ�����ߵĶ���ʱ����OAM=120�㣬���жϡ�BOF���AOM�������Ӷ��õ���ʱM������꣮
�������жϡ�OBFΪ����Ϊ120���ĵ�������������������AM=AO=2ʱ����M���C���غ�����BOF���AOM�������ô�ʱM�����������OM=OAʱ����M���C������ֱ��x=1�Գ�����BOF���AOM�������ô�ʱM����������MA=MOʱ����MΪ�����ߵĶ���ʱ����OAM=120�㣬���жϡ�BOF���AOM�������Ӷ��õ���ʱM������꣮
�������1����C��H��x������ͼ����
�ߡ�CDE�͡�OABΪȫ�ȵĵȱ��������������ǰ�CDE�Ʊ�AB���е�G��G��Ҳ��DE���е㣩����˳ʱ�뷽����ת180���õ���C��ED����AC��=OA=2����OAB=��BAC��=60�㣬���C��AH=60�㣬��AH=![]() AC��=1��C��H=
AC��=1��C��H=![]() AH=
AH=![]() ����C�䣨3��
����C�䣨3��![]() ����
����
��2���������߽���ʽΪy=![]() ���������a31=
���������a31=![]() �������a=
�������a=![]() ���������߽���ʽΪy=
���������߽���ʽΪy=![]() x��x��2������y=
x��x��2������y=![]() x2��
x2��![]() x��
x��
��3����BFΪ��G����������AB��BF������FAB=60�㣬��FA=2AB=4����F����2��0����
��OB=OA=AC��=BC��=2�����ı���AOBC��Ϊ��������B��1��![]() ������ֱ��BF�Ľ���ʽΪy=kx+b����F����2��0����B��1��
������ֱ��BF�Ľ���ʽΪy=kx+b����F����2��0����B��1��![]() ���������
���������![]() �������
�������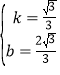 ����ֱ��BF�Ľ���ʽΪy=
����ֱ��BF�Ľ���ʽΪy=![]() x+
x+![]() ��
��
��4�����ڣ�
�����ߵĶԳ���Ϊֱ��x=1����x=1ʱ��y=![]() x2��
x2��![]() x=��
x=��![]() ���������ߵĶ�������Ϊ��1����
���������ߵĶ�������Ϊ��1����![]() ����
����
��OF=OB=2�����OBFΪ����Ϊ120���ĵ�������������AM=AO=2ʱ����M���C���غ�����BOF���AOM��������ʱM��3��![]() ������OM=OAʱ����M���C������ֱ��x=1�Գ�����BOF���AOM��������ʱM����1��
������OM=OAʱ����M���C������ֱ��x=1�Գ�����BOF���AOM��������ʱM����1��![]() ������MA=MOʱ����MΪ�����ߵĶ���ʱ����OAM=120�㣬��BOF���AOM��������ʱM��1����
������MA=MOʱ����MΪ�����ߵĶ���ʱ����OAM=120�㣬��BOF���AOM��������ʱM��1����![]() ����
����
��������������������M���������3��![]() ����1��
����1��![]() ����1����
����1����![]() ����
����

 �¿α�������������ҵ�������γ�����ϵ�д�
�¿α�������������ҵ�������γ�����ϵ�д�����Ŀ��ij�������м���ԭ��263ǧ�ˣ�����ԭ��314ǧ�ˣ��ƻ�����������ԭ������A��B���ֲ�Ʒ��100��������һ����Ʒ����Ҫ��ԭ�ϼ������ɱ����±���ʾ��
����ԭ�ϣ���λ��ǧ�ˣ� | ����ԭ�ϣ���λ��ǧ�ˣ� | �����ɱ�����λ��Ԫ�� | |
A��Ʒ | 3 | 2 | 120 |
B��Ʒ | 2.5 | 3.5 | 200 |
��1���ù������е�ԭ���ܷ�֤������Ҫ�����ܣ��м�������������������Ƴ�����
��2��������A��B���ֲ�Ʒ���ܳɱ�ΪyԪ����������A��Ʒx������д��y��x֮��ĺ�����ϵ�������ú���������˵����1�����������������ܳɱ���ͣ���������ܳɱ��Ƕ��٣�