题目内容
【题目】(探究与证明)
在正方形ABCD中,G是射线AC上一动点(不与点A、C重合),连BG,作BH⊥BG,且使BH=BG,连GH、CH.
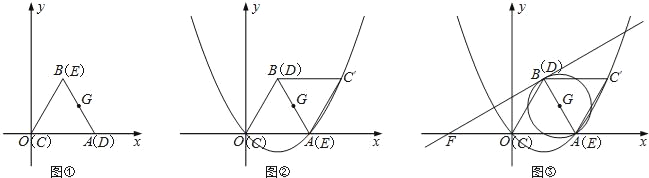
(1)若G在AC上(如图1),则:①图中与△ABG全等的三角形是 .
②线段AG、CG、GH之间的数量关系是 .
(2)若G在AC的延长线上(如图2),那么线段AG、CG、BG之间有怎样的数量关系?写出结论并给出证明;
(应用)(3)如图3,G在正方形ABCD的对角线CA的延长线上,以BG为边作正方形BGMN,若AG=2,AD=4,请直接写出正方形BGMN的面积.

【答案】(1)①△CBH,②AG2+CG2=GH 2(2)20+8![]()
【解析】
探究与证明(1)①由题意可得AB=BC,BG=BH,∠ABG=∠CBH 可证△ABG≌△BCH
②由△ABG≌△BCH可得AG=CH,∠ACH=90° 可得AG、CG、GH之间的数量关系.
(2)连接CH,可证△ABG≌△BCH,可得△CHG是直角三角形,则AG2+CG2=GH2,且HG2=BG2+BH2=2BG2,可得线段AG、CG、BG之间.
应用:(3)连接BD交AC于O,由正方形ABCD可得AC⊥BD,AO=BO=CO=2![]() ,则根据正方形GBMN的面积=BG2=GO2+BO2.可求正方形GBMN的面积.
,则根据正方形GBMN的面积=BG2=GO2+BO2.可求正方形GBMN的面积.
解:探究与证明:(1)①△CBH,②AG2+CG2=GH 2
理由如下:
∵ABCD是正方形
∴AB=CB,∠ABC=90°,∠BAC=∠BCA=45°
又∵GB⊥BH
∴∠ABG=∠CBH且BG=BH,AB=BC
∴△ABG≌△BCH
∴∠BAC=∠BCH=45°,AG=CH
∴∠GCH=90°
在Rt△GCH中,CH2+CG2=GH 2
∴AG2+CG2=GH 2
(2)

如图2,连CH
∵四边形ABCD是正方形
∴∠ABC=90°,AB=BC
∵∠GBH=90°
∴∠ABC+∠GBC=∠GBH+∠GBC
即:∠ABG=∠CBH
又∵BH=BG
∴△ABG≌△CBH
∴AG=CH,∠BCH=∠BAC=45°
∴∠ACH=∠ACB+∠BCH=45°+45°=90°
∴AG⊥CH
∴CH2+CG2=GH 2
∴AG2+CG2=GH2
∵HG2=BG2+BH2=2BG2
∴AG2+CG2=2BG2
应用:(3)如图连接BD交AC于O
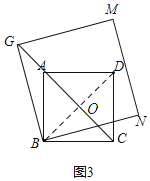
∵四边形ABCD 是正方形,AD=4,
∴AC=4![]() ,BO=AO=DO=CO=2
,BO=AO=DO=CO=2![]() ,AC⊥BD,
,AC⊥BD,
∴BG2=GO2+BO2,
∵S正方形GBNM=BG2=GO2+BO2=(2+2![]() )2/span>+(2
)2/span>+(2![]() )2=20+8
)2=20+8![]() .
.

【题目】学完“数据的收集、整理与描述”后,李明对本班期中考试数学成绩(成绩均为整数,满分为150分)作了统计分析(每个人的成绩各不相同,且最低分为50分),绘制成如下频数分布表和频数分布直方图(为避免分数出现在分组的端点处,李明将分点取小数),请你根据图表提供的信息,解答下列问题:
分组 | 频数 | 频率 |
49.5~69.5 | 2 | 0.04 |
69.5~89.5 | 8 |
|
89.5~109.5 | 20 | 0.40 |
109.5~129.5 |
| 0.32 |
129.5~150.5 | 4 | 0.08 |
合计 |
| 1 |

(1)分布表中![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)补全频数分布直方图;
(3)若画该班期中考试数学成绩的扇形统计图,则分数在89.5~109.5之间的扇形圆心角的度数是____![]() ;
;
(4)张亮同学成绩为109分,他说:“我们班上比我成绩高的人还有![]() ,我要继续努力.”他的说法正确吗?请说明理由.
,我要继续努力.”他的说法正确吗?请说明理由.