题目内容
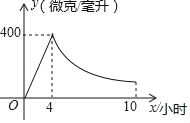
【题目】驾驶员血液中每毫升的酒精含量大于或等于200微克即为酒驾,某研究所经实验测得:成人饮用某品牌38度白酒后血液中酒精浓度y(微克/毫升)与饮酒时间x(小时)之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中酒精浓度上升和下降阶段y与x之间的函数表达式.
(2)问血液中酒精浓度不低于200微克/毫升的持续时间是多少小时?
【答案】(1)y=![]() (4≤x≤10).(2)6小时.
(4≤x≤10).(2)6小时.
【解析】
(1)当0≤x≤4时,设直线解析式为:y=kx,当4≤x≤10时,设反比例函数解析式为:y=![]() ,利用待定系数法即可解决问题;
,利用待定系数法即可解决问题;
(2)分别求出y=200时的两个函数值,再求时间差即可解决问题.
解:(1)当0≤x≤4时,设直线解析式为:y=kx,将(4,400)代入得:400=4k,
解得:k=100,故直线解析式为:y=100x,
当4≤x≤10时,设反比例函数解析式为:y=![]() ,将(4,400)代入得:400=
,将(4,400)代入得:400=![]() ,
,
解得:a=1600,故反比例函数解析式为:y=![]() ;
;
因此血液中药物浓度上升阶段的函数关系式为y=100x(0≤x≤4),
下降阶段的函数关系式为y=![]() (4≤x≤10).
(4≤x≤10).
(2)当y=200,则200=100x,
解得:x=2,
当y=200,则200=![]() ,
,
解得:x=8,
∵8﹣2=6(小时),
∴血液中药物浓度不低于200微克/毫升的持续时间6小时.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案【题目】射阳县实验初中为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
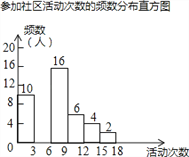
参加社区活动次数的频数、频率分布表
活动次数x | 频数 | 频率 |
0<x≤3 | 10 | 0.20 |
3<x≤6 | a | 0.24 |
6<x≤9 | 16 | 0.32 |
9<x≤12 | 6 | 0.12 |
12<x≤15 | m | b |
15<x≤18 | 2 | n |
根据以上图表信息,解答下列问题:
(1)表中a= ,b= ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?